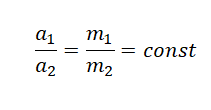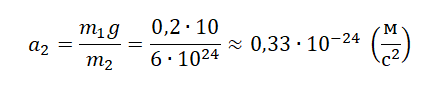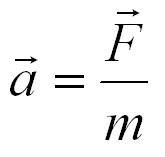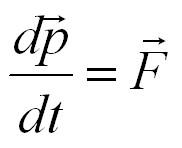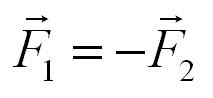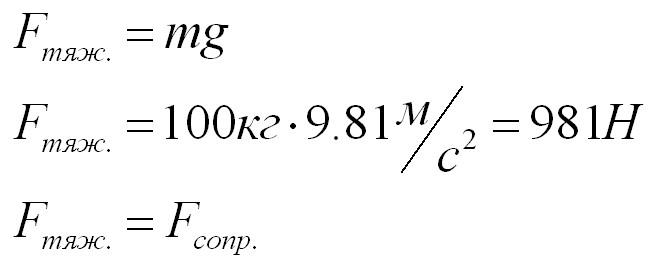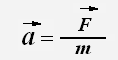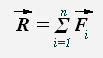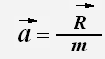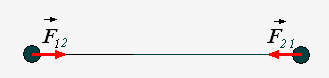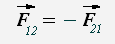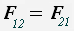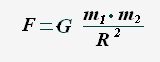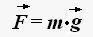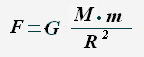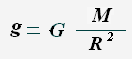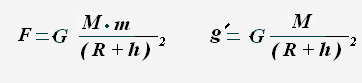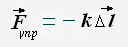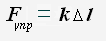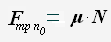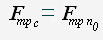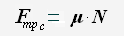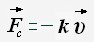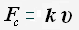Существуют такие системы отсчета в которых всякое тело будет сохранять
Первый закон Ньютона.
Ньютон сформулировал закон инерции, включив его в основу механики в качестве первого из трех законов. Поэтому этот закон называют первым законом Ньютона.
Первый закон механики, или закон инерции был сформулирован Ньютоном следующим образом:
Любое тело удерживается в состоянии покоя или равномерного прямолинейного движения, пока под действием приложенных сил не изменяет это состояние.
В окружении любого тела, покоится оно или движется, есть другие тела, некоторые из которых или все как-то действуют на тело, влияют на состояние его движения. Чтобы выяснить влияние окружающих тел, надо исследовать каждый отдельный случай.
Рассмотрим какое-либо покоящееся тело, не обладающее ускорением, а скорость постоянна и равна нулю. Допустим, это будет шарик, подвешенный на резиновом шнуре. Он находится в покое относительно Земли. Около шарика множество различных тел: шнур, на котором он висит, множество предметов в комнате и других помещениях и, конечно, Земля. Однако, действие всех этих тел на шарик не одинаково. Если, например, убрать мебель в комнате, это не окажет какого-либо влияния на шарик. Но если перерезать шнур, шарик под влиянием Земли начнет падать вниз с ускорением. Но пока шнур не был перерезан, шарик находился в покое. Этот простой опыт показывает, что из всех тел, окружающих шарик, только два заметно влияют на него: резиновый шнур и Земля. Их совместное влияние и обеспечивает состояние покоя шарика. Стоило устранить одно из этих тел — шнур, и состояние покоя нарушилось. Если бы возможно было убрать Землю, это тоже нарушило бы покой шарика: он стал бы двигаться в противоположном направлении.
Отсюда приходим к выводу, что действия на шарик двух тел — шнура и Земли, компенсируют (уравновешивают) друг друга. Когда говорят, что действия двух или нескольких тел компенсируют друг друга, то это значит, что результат их совместного действия такой же, как если бы этих тел вовсе не было.
Рассмотренный пример, как и другие подобные примеры, позволяют сделать следующий вывод: если действия тел компенсируют друг друга, то тело под влиянием этих тел находится в состоянии покоя.
Таким образом, мы пришли к одному из основных законов механики, который называют первым законом Ньютона:
Существуют такие системы отсчета, относительно которых движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела или действие других тел компенсируется.
Однако, как выяснилось со временем, первый закон Ньютона выполняется только в инерциальных системах отсчета. Поэтому с точки зрения современных представлений закон Ньютона формулируют следующим образом:
Системы отсчета, относительно которых свободное тело при компенсации внешних воздействий движется равномерно и прямолинейно, называют инерциальными системами отсчета.
Свободным телом в этом случае называют тело, на которое другие тела не оказывают воздействия.
Необходимо помнить, что в первом законе Ньютона рассматриваются тела, которые могут быть представлены в качестве материальных точек.
Законы Ньютона. Динамика.
теория по физике 🧲 динамика
Три закона Ньютона
Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.
Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.
Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.
Основное утверждение механики
Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:
Основное утверждение механики
Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.
Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).
Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.
Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.
Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.
Первый закон Ньютона
Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.
Первый закон Ньютона
Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.
Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).
Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.
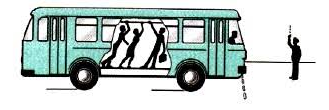
Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.
Второй закон Ньютона
В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.
Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.
Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).
Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.
Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.
Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.
Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.
Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.
Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.
Второй закон Ньютона
Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.
где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела
Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.
Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:
F = ma = 0,2 ∙ 9,8 = 1,96 (Н)
Равнодействующая сила
Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.
Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.
В этом случае второй закон Ньютона формулируется так:
Второй закон Ньютона через равнодействующие силы
Если на тело действует несколько сил, но их равнодействующая R будет равна произведению массы на ускорение этого тела.
Правила сложения сил и их проекций
Сложение двух сил, направленных вдоль одной прямой в одну сторону
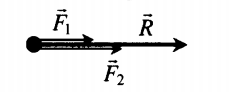
Равнодействующая сила сонаправлена с обеими силами.
Сложение двух сил, направленных вдоль одной прямой во взаимно противоположных направлениях
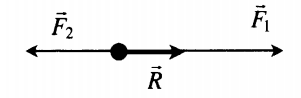
Равнодействующая сила направлена в сторону направления большей по модулю силы.
Сложение двух сил, перпендикулярных друг к другу
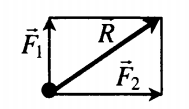
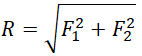
Сложение двух сил, расположенных под углом α друг к другу
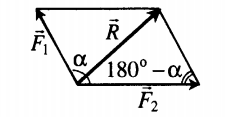
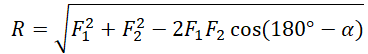
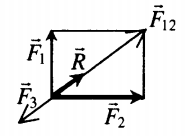
Сложение трех сил
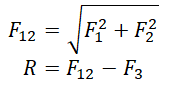
Сложение проекций сил
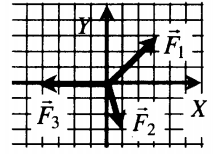
Проекция на ось OY:
Третий закон Ньютона
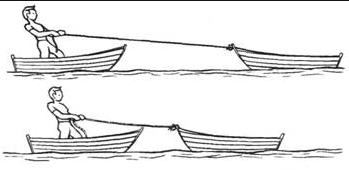
Когда одно тело действует на другое, начинается взаимодействие этих тел. Это значит, если тело А действует на тело В и сообщает ему ускорение, то и тело В действует на тело А, тоже придавая ему ускорение. К примеру, если сжать пружину руками, то руки будут чувствовать сопротивление, оказываемое силой упругости пружины. Если же, находясь в лодке, начать тянуть за веревку вторую лодку, то обе лодки будут двигаться навстречу друг другу. То есть, вы, находясь в своей лодке, тоже будете двигаться навстречу второй лодке.
Иногда на тело действует сразу несколько сил, но тело продолжает покоиться. В этом случае говорят, что силы друг друга компенсируют, то есть их равнодействующая равна нулю.
Две силы независимо от их природы считаются равными по модулю и противоположно направленными, если их одновременное действие на тело не меняет его скорости.
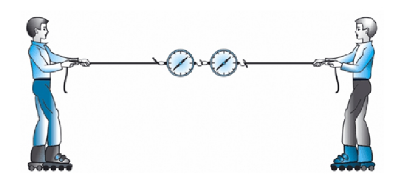
Примером такого явления служит ситуация, когда при перетягивании каната его никто не может перетянуть в свою сторону. Если взять два каната и присоединить между ними два динамометра, а затем начать игру в перетягивание, выяснится, что показания динамометра всегда будут одинаковыми. Это значит, что независимо от масс и придаваемых ускорений два взаимодействующих тела оказывают друг на друга равные по модулю силы. В этом заключается смысл третьего закона Ньютона.
Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.
Используя второй закон Ньютона, третий закон механики можно переписать иначе:
Отношение модулей ускорений a 1 и a 2 взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил.
Согласно третьему закону Ньютона модули сил, с которыми взаимодействуют Земли и яблоко, равны. Поэтому:
Пусть тело 1 будет яблоко, а тело 2 — Земля. Тогда a1 будет равно g. Отсюда ускорение, с которым движется Земля к падающему на нее яблоку, равна:
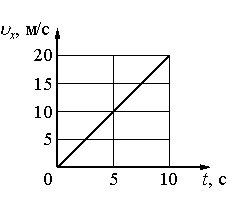
Законы Ньютона для «чайников»: объяснение 1, 2, 3 закона, пример с формулами
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих «Математических началах натуральной философии».
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
В самом конце предлагаем посмотреть видеоурок на тему «Законы Ньютона».
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Существуют такие системы отсчета в которых всякое тело будет сохранять
Официальный сайт АНО ДО Центра «Логос», г.Глазов
Динамика немного о физике:
Гравитационная и инертная массы тождественны друг другу, поэтому будем говорить просто о массе.
1. Масса составного тела равна сумме масс составляющих его частей.
2. Масса системы тел остается неизменной при любых процессах происходящих ней (закон сохранения массы).
Результат действия силы зависит от направления, модуля силы и от точки приложения силы. Результатом действия силы являются изменение скорости тела или деформация.
Первый закон Ньютона
Существуют такие системы отсчета относительно которых поступательно движущиеся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действие других тел скомпенсировано.
Инерциальность системы отсчета определяется опытным путем, для этого устанавливается отсутствие ускорения, существование которого невозможно объяснить.
В настоящее время экспериментально подтверждено, что практически инерциальна гелиоцентрическая система отсчета, связанная с центром Солнца и тремя «неподвижными» звездами.
Любая другая система отсчета, движущаяся относительно инерциальной равномерно и прямолинейно сама является инерциальной.
Второй закон Ньютона.
Ускорение, приобретаемое материальной точкой в инерциальной системе отсчета пропорционально действующей на точку силе и обратно пропорционально ее массе и по направлению совпадает с силой.
Если на тело одновременно действует несколько сил, то они могут быть заменены одной силой, называемой равнодействующей и равной их геометрической сумме.
Результирующее ускорение, приобретаемое точкой от воздействия нескольких сил определяется по второму закону Ньютона:
Третий закон Ньютона.
В инерциальной системе отсчета силы, с которыми две материальные точки действуют друг на друга, направлены вдоль одной прямой, соединяющей эти точки. Эти силы равны по модулю и противоположны по направлению.
Обе силы приложены к разным телам и являются силами одной природы.
Гравитационное взаимодействие между телами осуществляется при посредстве гравитационного поля.
Гравитационные силы направлены вдоль одной прямой, соединяющей взаимодействующие точки, т.е. являются центральными силами.
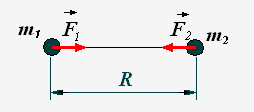
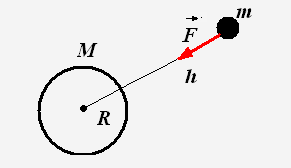
Закон всемирного тяготения:
М ежду двумя материальными точками действуют силы взаимного притяжения, пропорциональные произведению масс точек, обратно пропорциональные квадрату расстояния между ними.
Сила, с которой Земля притягивает тела называется силой тяжести.
На основании закона всемирного тяготения
Если тело массой m находится на высоте h от поверхности Земли, то
Сила, возникающая при упругой деформации тела, называется силой упругости.
Рассмотрим деформации сжатия и растяжения. Эти деформации характерны для нитей, пружин, стержней и т.п. При этих деформациях сила упругости направлена вдоль линии действия внешней силы.
Для упругой деформаций сжатия и растяжения сила упругости определяется согласно закону Гука.
Сила упругости возникающая в деформированном тела прямо пропорциональна вектору деформации и противоположна ему по направлению.
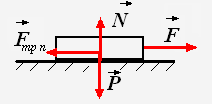
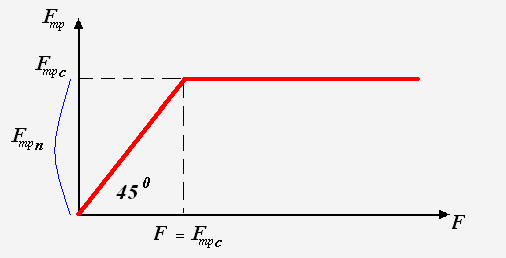
При увеличении значения внешней силы от нуля до некоторого значения движения тела не возникает, следовательно, возникающая сила трения компенсирует внешнюю силу. Т.к. модуль силы трения покоя равен модулю внешней силы, то сила трения покоя принимает значения:
Сила, действующая на тело при его поступательном движении в жидкости или газе, называется силой сопротивления.
Сила сопротивления зависит от скорости тела относительно внешней среды и направлена противоположно вектору скорости тела.
- Существуют такие примитивы векторной графики как
- Существуют такие системы отсчета относительно которых поступательно движущееся тело сохраняет свою