на сколько частей делится торт
Как красиво разрезать торт на равные части: простые методы и рекомендации
Какие инструменты понадобятся для резки торта
Нож для нарезки томатов
Это сейчас Бубличкина буквально приходит в ужас при виде небрежно покромсанного десерта. А раньше, когда она еще не знала, как разрезать круглый торт, все было вроде бы замечательно и прилично. Так было, пока какой-то кондитер не показал Анюточке, как он управляется с десертом при помощи ножа для нарезки свежих помидоров.
Многие из нас склоняются к использованию простого поварского ножа, считая, что его острое лезвие справится с задачей на ура. Да и, честно говоря, перед тем, как разрезать большой торт, под рукой ничего другого-то и нет. Но послушаем, что говорит Анюточка.
Как разрезать торт в домашних условиях: три верных метода
Быстрое охлаждение
В основном мы любим кушать пирожные комнатной температуры. Тем не менее, не бойтесь немного охладить торт перед нарезкой:
После того, как куски торта будут выложены на тарелку, они быстро погреются. Если вы не уверены в этом, подождите еще минут пять, прежде чем подавать на стол.
Горячий способ разрезать торт: просто нагрей воду
Кондитерские уловки
Леска
Если вы слышали об использовании зубной нити для нарезки булочек или чизкейка, то этот трюк вас не удивит. Оказывается, простая леска отлично справляется с делением пирога на кусочки. Используйте чистую прочную леску, длина которой должна быть не меньше диаметра торта плюс 10-15 см. Теперь о том, как резать:
Постарайтесь убрать беспорядок
Иногда вроде бы и знаем, как разрезать торт на равные части, и инструмент выбрали правильный, и надрезы делаем максимально осознанно, но в итоге все равно имеем крошки и размазанную глазурь. В таких случаях Бубличкина говорит: «Не парьтесь! Ваш пирог по-прежнему восхитителен, с кремом и всеми остальными прибамбасами».
Если вы часто печете десертные штучки, то есть резон купить кондитерский пинцет. Он наверняка пригодится, если вы полны решимости получить куски идеальной формы. С его помощью можно удалить все крошки и крем, где он неуместен.
У Анюточки есть еще один вариант, причем он проще и даже очень вкусный. Достаньте из холодильника мороженое или взбитые сливки и подавайте свой Torte à la mode. Гости так будут увлечены многослойным десертом, что им будет не до крошек!
Как разрезать торт на равные части, чтобы никого не обделить
Порезать-то мы порежем, а вот насколько справедливо – вопрос. Хорошо, если у нас компания из 4-6 человек, а ну как их будет 8-10? Рассчитывать на то, что контингент уже тепленький или руководствоваться формулой «от каждого по способностям, каждому – по труду» не стоит. Поэтому вкратце пробежимся по способам нарезки.
Круглый
Самый элементарный метод: разрезать пирог пополам, потом каждую половину разделить еще на два куска. Если есть нужда, оставшиеся части делят еще на несколько разных долей. 
Разрезание ромашкой – более сложный способ. В центре торта вырезают большой круглый кусок. Делают это при помощи какой-нибудь подходящей формы, на крайний случай можно воспользоваться блюдцем, прислонив его к центру изделия. Внешнюю часть нужно разделить на равные куски, а с серединой поступают по схеме, описанной выше.
Прямоугольный
Обычно десерты прямоугольной формы профессионалы режут на ромбики – так они выглядят аппетитно и, чего уж там говорить, эстетично. Но для этого нужен опыт и твердая рука, а откуда этому взяться у работающих домохозяек? Но они тоже хотят знать, как аккуратно и ровно разрезать торт на одинаковые кусочки.

Поэтому будем действовать проще: сделаем нужное количество продольных резов вдоль длинной стороны пирога, а затем разделим их поперечными «пропилами».
Квадратный
С квадратным десертом дело обстоит проще. Первое, что делают – проводят через центр торта два перпендикулярных друг к другу разреза. 
Получается четыре равных куска, которые можно еще раз поделить пополам или на четыре части по той же технологии.
Если не боитесь экспериментов, попробуйте разрезать десерт по диагонали, а затем на треугольные кусочки.
Нарежь торт безупречно!
Независимо от того, приготовили ли вы дачный Наполеон или другой слоеный пирог, нарежьте его как опытный кондитер, используя рекомендации Бубличкиной:
Как красиво порезать торт [11 вариантов]
Эта статья будет полезна всем, кто планирует лакомиться сам или угощать кого-то таким десертным блюдом, как торт. Да, именно о том, как резать торт, в том числе и как правильно резать свадебный торт, пойдет речь в этой статье. Поэтому если вы будущая невеста или будущий жених, то обязательно прочтите ее.
С инструментами разобрались, перейдем непосредственно к процессу нарезания. Все схемы деления торта на кусочки можно структурировать по форме, высоте и по количеству предполагаемых порций. То есть существуют схемы для нарезания круглых, квадратных, прямоугольных, многоярусных, одноярусных но высоких, для больших и маленьких компаний.
Круглый
Если вам необходимо поделить круглый торт на равные части, сделать это можно следующими способами.
Клиньями
Это один из самых известных и часто используемых методов. Чтобы нарезать клиньями, нужно отыскать центр торта, и постепенно продвигаться острием ножа от центра к краям. Но такая схема подходит только для тортиков небольшого размера, иначе порции будут совсем большими.
Второй вариант получить ровные треугольные кусочки довольно прост в исполнении. Нужно пройдясь ножом от одного края к противоположному краю поделить его на два полукруга по диаметру, далее каждый полукруг еще на пополам так, чтобы получилось четыре сектора. И затем каждую четвертинку проходя от края через центр к другому краю круга, еще раз поделить пополам. Таким способом быстро и просто образуются равные треугольные ломтики.
Ромбиками
Если вы хотите правильно нарезать бисквит ромбиками, необходимо десерт сначала разделить горизонтальными линиями на полосы. После этого пройтись ножом диагонально полученным ранее полоскам. Так ромбики получатся максимально одинаковыми по размеру, нежели вы будете каждый ромбик намечать и отрезать отдельно. От диаметра торта зависит какие полосы нужно наметить, чтобы были красивые ромбики.
Квадратный
Квадратные и прямоугольные кондитерские изделия не только потрясающе выглядят, потому что дают простор для фантазии в оформлении поверхности, но и довольно легко делятся на равные порции. Именно поэтому частенько свадебные торты заказывают квадратными. Их очень просто разделить можно двумя формами:
Кубиками
Для этого проведите два или три длинных продольных разреза (в зависимости от ширины десерта) с одинаковым расстоянием, а затем несколько раз разрежьте торт поперек, таким образом деля длинные полосы на равные квадратные порции.
Треугольниками
Нарежьте торт на прямоугольные куски, как написано выше. Помните, что их должно быть в 2 раза меньше, чем гостей. Затем каждый прямоугольник просто разрежьте по диагонали и подавайте десерт к столу. Заметьте, вначале при таком способе лучше поделить именно на прямоугольники, а не на квадраты, чтобы в результате получились более удобные для подачи треугольные небольшие дольки.
Нестандартная форма
Кондитерский мир не стоит на месте, каждый сезон появляются новые тренды, которые поражают и удивляют любителей сладостей своим внешним видом. Среди заказов бывают торты:
Выглядят такие торты безусловно эффектно, а фото и видео с праздника смотрятся особенно красочно. Однако при необходимости нарезать его встает вопрос: «Как сделать, чтобы всем досталось по одинаковой доле, и чтобы это было красиво?» Особенно такой вопрос актуален на торжествах. Обращали внимание когда стоя перед большим свадебным тортом нестандартной формы молодожены переглядываются друг с другом в надежде, что партнер знает как правильно поступить? Или юбиляр, который крутится вокруг торта в виде числа его возраста, не зная с какой стороны приступить к нарезанию?
Во избежание таких неловких ситуаций, запоминаем универсальные варианты нарезания нестандартного торта.
Сетка
Изделие по форме напоминающее очертания овала и сердца удобнее всего разрезать по длине на полосы нужного размера, а потом разрезать их на прямоугольники.
Ромашка
Если же речь идет о кондитерских изделиях, выполненных сложным силуэтом, то их лучше всего резать методом «ромашка».
Для этого визуально отделяют середину в круглый вырез, и часть по периметру нарезают на пропорциональные кусочки, не затрагивая центр. После того как крайние куски разделены, приступают к центральной части, которую можно поделить как стандартный торт круглой формы. По фото выше визуально понятно, что количество делений на круги по схеме «ромашка» зависит от размера угощения.
Ярусный торт
Но бывают многоярусные торты имеющие два-три яруса, расположенных прямо друг на друге. В таком случае молодым не помешает знать, как правильно резать ярусный торт, чтобы не разрушить всю конструкцию.
1) Самый первый верхний ярус необходимо аккуратно снять. Если это свадебный торт, традиционно его оставляют жениху и невесте. Затем сам торт начинают разрезать со второго яруса, постепенно продвигаясь вниз
Советы кондитера
В завершение добавим несколько немаловажных советов касательно главного десертного блюда любого события, которые значительно облегчат процесс подготовки и организации ваших праздников.
Чтобы точно знать какой по весу торт заказывать рассчитайте примерно 100-150 гр на гостя. Но если выбираете декор мастикой, помните, что она очень тяжелая, соответственно лучше делать кусочки весом около 200 гр.
Существует любопытный способ, позволяющий красиво разделить практически любой торт так, чтобы он дольше оставался свежим, края не высохли, а крем не заветрился. Он носит название «Математического метода Ф.Гальтона». Для начала нужно вырезать и вынуть полоску из середины. Затем необходимо совместить оставшиеся две половинки и снова вырезать полоску из середин обеих половин. В итоге должны остаться четвертушки, которые разделены радиально. Их нужно всего лишь совместить друг с другом, чтобы держать кондитерское изделие собранным. А вырезанные полоски нарезаем на кубики или ромбики и подаем к столу. Такой метод особенно актуален, если куплен большой торт, и есть большая вероятность, что лакомство останется несъеденным. Такое деление подойдет даже для двухъярусных свадебных конструкций.
По фото ниже вы можете посмотреть и взять себе на заметку эту схему
Старайтесь заказывать не слишком высокие торты. Лучше пусть будет средней высоты, но широкий в диаметре. Это касается и свадебных десертов. Понятное дело, одноярусные свадебные «башенки» сейчас на пике трендов, но как резать высокий торт? В сети много видео инструкций для разрезания высокого торта, но на наш взгляд они не совсем эстетичны в процессе, и требуют дополнительных затрат времени и посуды. Судя по реакциям в комментариях на нашей страничке инстаграм высокие экземпляры несомненные фавориты, но все таки конструкцию небольшого размера намного проще распределить и красиво подать.
Фигурки из шоколада «жених и невеста», сердечки, бантики, цветочки, или любые другие фигурки из мастики, шоколада или сахара не стоит разрезать вместе с коржами. Украшения на поверхности торта правильнее всего снять перед нарезкой и подать вместе с порцией торта на стол новобрачных. А если они сделаны из несъедобных материалов, то молодым можно сохранить их на память и использовать в день годовщины свадьбы.
Учитывайте состав нарезаемого торта при создании условий хранения до его подачи. Если был заказан мягкий бисквит с ягодной или фруктовой добавкой в начинке, то лучше оставить его в холодильнике на весь день, чтобы не потек. А изделия с карамельными кремами, твердыми коржами наподобие дакуаза, или нугой лучше минут 20-30 подержать в тепле перед подачей. Организаторы свадебных и других торжество обязательно должны обращать внимание и знать о таких особенностях.
Разрезание двухъярусного торта на свадьбе для удобства молодоженов и экономии времени лучше доверить сотрудникам заведения. Не беспокойтесь, чаще всего они опытны в этом деле и спокойно нарежут ваш десерт на столько кусочков, сколько нужно.
Торт 1,2,3.. кг на сколько человек & Сколько кг торта нужно на 10,15,20.. человек
Количество гостей / вес торта
Сколько нужно кг торта на определенное количество человек.
| Бисквитный | Муссовый | |
| Количество приглашенных | Вес, кг | |
| 8 | 1,5 | 1 |
| 10 | 2 | 1,5 |
| 15 | 3 | 2,5 |
| 15-20 | 3-4 | 2,5-3 |
| 20-30 | 4-6 | 3-4 |
| 30-40 | 6-8 | 4,5-6 |
| 40-50 | 8-9 | 6-7 |
| 50-70 | 9-11 | 7,5-9 |
| 70-90 | 11-14 | 9-12 |
| 90-110 | 14-16 | 12-13 |
| 110-130 | 16,5-19,5 | 13-14 |
| 130-150 | 19,5-22,5 | 14-15 |
| 150-170 | 22,5-25,5 | 15-16 |
| 170-190 | 25,5-28,5 | 16-17 |
| 190-200 | 28,5-30 | 17-19 |
| 200+ | 30+ | 19+ |
При количестве гостей до 50 рассчитывают по 200 г торта на человека. Если приглашенных больше, то по 150 г на каждого.
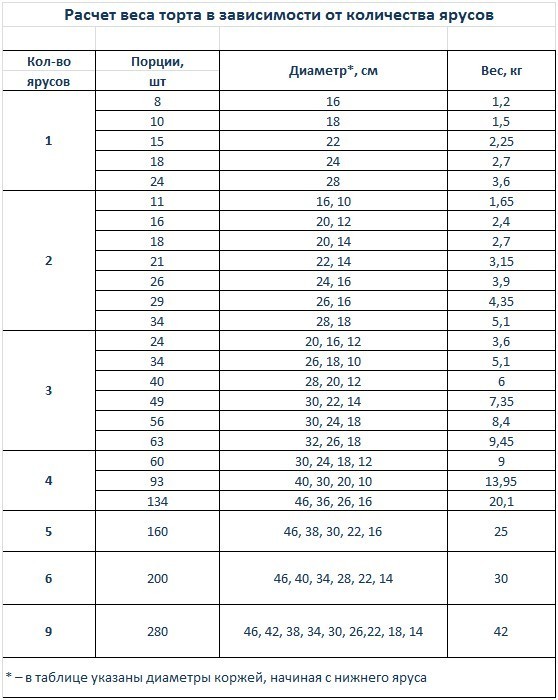
Вес торта в зависимости от кол-ва ярусов
Сколько нужно ярусов на 10, 15, 20, 25 человек.
В кондитерском деле есть понятие фальш-ярус – декоративный этаж, призванный придать десерту большей привлекательности.
Фальш-ярус часто используют, когда необходим двухъярусный торт, но нужно ограничиться небольшим объемом.
Как рассчитать вес торта на количество гостей
Считают из пропорции 150-200 г угощения на взрослого и 100-150 г на ребенка.
Точно рассчитать массу конкретного кондитерского шедевра сложно, поскольку он зависит от многих факторов. Влияет начинка, плотность коржей, наличие декора.
Видео — как рассчитать торт на свадьбу
Самый старый торт в мире имеет больше 100 лет выдержки. Его приготовили еще в 1898 году. Во времена Второй мировой войны на нем возникла трещина от взрывной волны.
Как математики нарезают торт?
Как лучше всего нарезать торт? Если вы не профессиональный свадебный планировщик, то наверняка не часто размышляли над таким вопросом. Вы можете подумать, что ответ довольно прост. Нужно просто посчитать количество гостей, сидящих за столом, и поделить десерт на одинаковые куски. Всевозможные диеты и аллергии на глютен могут усложнить ваши вычисления, но в конечном счете этот процесс вряд ли покажется сложным математическим действием.
Тем не менее, как бы парадоксально это ни звучало, речь идет именно о высшей математике, и вы определенно забыли задать себе несколько важных вопросов.
К примеру, гарантирует ли ваш способ нарезки торта, что никто не покинет вечеринку, почувствовав себя обделенным? Предприняли ли вы какие-то шаги, дабы убедиться в том, что каждый посетитель будет в равной степени удовлетворен своим отдельно взятым ломтиком?
Как видите, сейчас мы говорим не просто о торте. В контексте решения проблемы «справедливого распределения», затрагивающей математику, политологию и экономику, торт представляет собой нечто большее, чем обыкновенный десерт. Торт — это многоэтажный дом с квартирами, которые следует разделить между придирчивыми жильцами. Торт — это бракоразводный процесс с высокими отступными. Торт — это охваченная гражданской войной страна.
Начиная с XVII века, теоретики занимаются разработкой методов, которые бы позволяли делить необходимые нам вещи в соответствии с жестким формализмом математики и нашими субъективными представлениями о справедливости. Все это время торт использовался в качестве мощной метафоры для всего ценного, исчерпаемого и делимого в этом мире.
И теперь, с учетом последних достижений в области теории справедливого распределения (fair division theory) и информатики, все больше исследователей хотят сделать эти методы доступными для неосведомленной общественности. Чтобы всего одним нажатием кнопки вы могли бы порезать торт как настоящий математик.
Принцип справедливого деления
Детям уже давно известен лучший способ разделить объект на две части. Этот метод называется «Я разделяю, ты выбираешь», и вы наверняка использовали этот алгоритм справедливого деления в далеком детстве. Гениальность данного подхода заключается не только в том, что он достаточно прост для применения, но и в том, что при определенных обстоятельствах он дает объективные результаты.
Человек, применяющий его, знает, что другой выберет себе лучший кусок, поэтому старается разрезать торт (бутерброд или что-либо еще) как можно более справедливо. Таким образом, обе стороны гарантированно получают порции, которые, по их мнению, являются примерно одинаковыми.
Экономисты и математики нарекли этот метод «свободным от зависти» и таким определением они попали точно в цель. Если у вас есть ванильный торт, и вам нужно разделить его между двумя людьми, каждый из которых одинаково любит сладкое, то, чтобы никто не начал завидовать, торт нужно разделить пополам. Оба получат равный кусок торта, и никаких математических талантов для такого разделения не нужно.
Метод «Я разделяю, ты выбираешь» работает не только для материальных вещей (торты и арахисовое масло). Как показал популярный писатель Мартин Гарднер в 1978 году, домашние обязанности также можно распределить, если один человек делит каждую задачу на две части, а другой выбирает одну из них.
Этот метод также используется юристами. При заключении контрактов на совместную собственность, адвокаты часто прибегают к денежному аналогу принципа «Я разделяю, ты выбираешь». Когда люди при разводе делят собственность, один партнер называет цену, а другой решает, хочет ли он её выкупить или продать.
Как пишет Джеймс Ф. Ринг, «инициирующая сторона ставит своего противника в положение, когда наиболее разумная стратегия для него заключается в том, чтобы честно оценить собственность и закончить спор».
Ринг убедился в этом на собственном опыте. Являясь соучредителем Fair Outcomes, компании, специализирующейся на оказании помощи людям при разводах, Ринг и Стивен Брамс нашли множество применений метода «Я разделяю, ты выбираешь».
В обзоре способов справедливого разделения, опубликованных на сайте nautil.us, научный писатель Эрика Кларрайх приводит один любопытный пример. В случае спора при расторжении брака или отношений, алгоритм, который Ринг и Брамс называют «Справедливая покупка-продажа», предполагает, что каждый партнер одновременно называет свою цену.
«Если Джон предложит 110 000 долларов, а Джейн предложит 100 000 долларов, тогда Джон, предложивший более высокую цену может выкупить вещь у Джейн за 105 000 долларов», — объясняет Ринг. «Каждый участник в результате получает что-то — деньги или вещь — по цене, которая лучше, чем его предложение».
Этот метод нашел место даже в международном морском праве. В 1970-х годах, когда государства готовились к будущему, в котором подводная добыча ископаемых станет крупной отраслью, развивающиеся страны были обеспокоены тем, что технологически более развитые корпорации приобретут права на разработку наиболее ценных морских участков.
Решение было предложено и ратифицировано в Конвенции по морскому праву. Теперь, если компания хочет добывать ресурсы с морского дна, она должна сначала разделить участок на две части. После чего менее развитая сторона выбирает один из них.
«Свобода от зависти»
Но, как может сказать любой ученик начальной школы, существуют такие конфликты, справиться с которыми не в состоянии даже способ «Я разделяю, ты выбираешь».
Возвращаясь к кулинарной метафоре, представьте себе, что рассматриваемый торт не простой ванильный (допустим, вдоль левого края были размещены несколько кусочков клубники), и что голодные гости за столом имеют разные предпочтения (может быть, один человек предпочитает фрукты, а другой любит выпечку).
Если пирог будет делить любитель клубники, он может разделить его на две половины, оставив равное количество клубники на каждой. Так он получит свою долю фруктов независимо от выбора другого человека. Поскольку любитель выпечки собирается выбросить свою клубнику, для него тоже не имеет значения, какую половину выбрать. В результате никто не будет завидовать.
Но всё же есть кое-что неудовлетворительное в подобном исходе. В частности, экономисты назвали бы этот результат «неэффективным», потому что торт можно было разрезать таким образом, чтобы сделать по крайней мере одного из участников счастливее, не причинив никому вреда. В приведённом примере можно было сделать так: любитель ягоды мог поменять часть своего пирога на клубнику. Всем было бы лучше.
Значит, разделение было неправильным? Ведь лучше, если бы он оставил себе больше клубники?
Предположим другую ситуацию. Любитель клубники просто отсекает меньшую покрытую ягодами половину. Таким образом, он гарантированно получит либо меньший кусок с большим количеством ягоды (что было бы хорошо, потому что он любит клубнику), либо больший кусочек без ягод (что тоже неплохо, потому что, несмотря на отсутствие ягод, он все же получает больше пирога).
На этот раз выбор для его друга очевиден. Он выберет большую часть торта.
Теперь результат можно назвать эффективным, потому что кусочки торта нельзя было бы поменять, не сделав хотя бы одну из сторон неудовлетворенной. Более того, в результате никто никому не завидует. Ни у одной из сторон нет причин хотеть поменять свой кусок. В теории нет причин для зависти.
И тем не менее, сложность людской психологии запутывает математическую выстроенную модель человеческого поведения. Вышеприведенное решение теоретически может иметь последствия, противоречащие нашему чувству справедливости. Поклонник клубники в любом случае не проиграет (он получает кусочек, который, по его мнению, составляет 50% от стоимости торта), в то время как любитель торта получает большую часть торта, то есть выигрывает в сделке.
Как разделить торт между тремя и более людьми
Десятилетиями теоретики тщетно пытались найти справедливое решение проблемы деления. Ведь приглашение к столу дополнительных претендентов на торт вводит еще большую сложность.
В 1940-х годах польский профессор Хьюго Штайнхаус подошел к этому вопросу с математической строгостью. Спросив себя, существует ли вариант метода «Я разделяю, ты выбираешь» для трех или более человек, он в конечном итоге придумал то, что теперь называется «методом одинокого разделителя».
Проиллюстрируем его суть на примере. Представьте себе трех потенциальных покупателей торта. Один из них выбирается наугад. Он становится «одиноким разделителем», и его просят разделить торт на три части. Как и в случае с «Я разделяю, ты выбираешь», он не знает, какой кусочек ему суждено получить, и поэтому пытается разделить торт на три одинаково желаемых ломтика.
Остальным двум участникам, выборщикам, предлагается записать, какие из кусочков они бы хотели. Затем списки сравниваются. Если они хотят разные кусочки, то игра окончена: каждый из них получает то, что хотел, а первый разделитель получает третий кусок.
Если же выборщики хотят один кусок, то разделителю дается одна из двух не востребованных частей, а два оставшихся куска соединяются. Теперь у нас есть один маленький торт, два голодных конкурента и метод «Я разделяю, ты выбираешь», который и решит их проблему.
Метод Штайнхауса привлекательно прост и может быть расширен до более чем трех человек, но он не гарантирует результатов, в которых не было бы зависти. Для этого требуется более сложная математика.
Торт из треугольников
Фрэнсис Су получил докторскую степень по математике в Гарварде в конце 1990-х, когда Брэд Манн, его друг и кандидат в докторанты, пришел к нему со своей проблемой.
Как и большинство студентов в районе Кембриджа, Манн снимал тесный домик с несколькими знакомыми. Естественно, их мнения расходились в том, кто должен получить комнату больших размеров. Манн пришел к Су с вопросом, как выйти из тупика.
В то время как большинство из нас предложило бы бросить жребий, Су, который теперь является профессором в колледже Харви Мадд и Президентом Математической ассоциации Америки, предложил оригинальное решение.
«Когда он рассказал мне о своем затруднительном положении, я сказал:«Это математический вопрос!», — рассказывает Су. В частности, это был вопрос справедливого разделения.
Возможно, решение Су было не очень полезным для Манна, но спустя несколько лет Су опубликовал статью на эту тему, в которой он смог доказать, что в доме, разделенном в соответствии с его методом, комнаты и арендная плата могут быть разделены так, чтобы никого не обидеть.
Статью Су новаторской сделало то, что он использовал сложный математический аргумент 1920-х годов, названный «леммой Спернера». Изначально лемма не имела ничего общего с арендой или тортами. Она относилась к треугольникам.
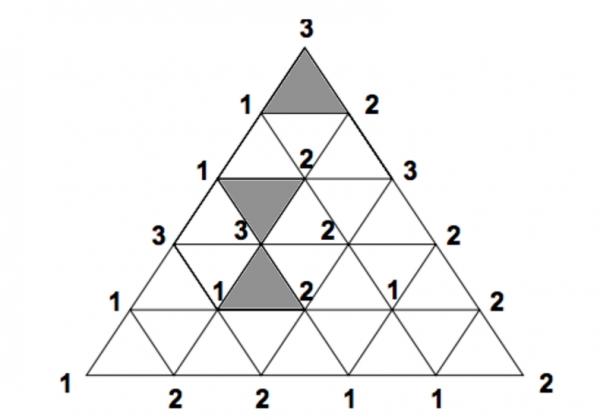
Представим себе, что у вас есть большой треугольник, как на рисунке выше. Каждую из вершин треугольника обозначим числами (в данном случае 1, 2 и 3). Треугольник затем разделяется на ряд меньших треугольников, и их вершинам также присваиваются числа.
Но здесь есть сложность. Любая вершина вдоль края большего треугольника должна делиться своим числом с одной из двух точек в конце этого края. Например, в нижней части треугольника могут быть только 1 и 2, потому что они расположены между двумя точками большего треугольника, которые обозначены 1 и 2. Аналогично, левая сторона треугольника может иметь только метки 1 и 3, в то время как правая сторона получает только 2 и 3.
Согласно «лемме» (мини-теореме), если все вышеприведенные условия верны, то во всей сетке перекрещивающихся вершин должен быть хотя бы один треугольник, который имеет разные числа в каждой из трех его точек. На рисунке выше таковых три.
Какое это имеет отношение к ренте? В нахождении этой связи и заключалось прозрение Су.
В статье треугольник переосмысливается как все возможные комбинации цен на комнаты, разделенные между тремя комнатами. Например, точка в верхней части треугольника может представлять собой ситуацию, когда один из соседей оплачивает всю аренду в комнате А, а остальные не платят ничего за оставшиеся две комнаты В и С. Аналогично, точка в левом углу большого треугольника будет представлять собой ситуацию, когда житель комнаты B отдает всю арендную плату. Перемещение в центр треугольника соответствует более справедливым распределениям ренты между тремя комнатами.
Су назначил каждого из жителей дома «владельцем» вершины (ценовой комбинации).
Математический алгоритм решения проблемы Су начинается с вершины за пределами треугольника с вопроса: «Если бы ренту нужно было разделить в соответствии с этой ценовой схемой, в какой комнате ты бы жил?» В зависимости от ответа, этому пункту будет дано число (1, 2 или 3). Затем алгоритм может «переместиться» на новую комбинацию «цена и комната», расположенную глубже внутри треугольника, где тот же вопрос будет задан другому жильцу.
Процедура будет продолжаться до тех пор, пока не будет найдена схема ценообразования, в которой каждый житель согласится жить в разных комнатах при определенных ценах. Графически этот пункт будет существовать в треугольнике, в котором вершины были бы помечены разными цифрами. Помните, что согласно лемме Спернера такой треугольник должен существовать.Таким образом, гармония возможна.
Идея Су стала настоящим открытием. В 2014 году New York Times даже сделал калькулятор арендной платы, используя алгоритм Су.
«Алгоритма справедливости» не существует
Алгоритм Фрэнсиса Су не является единственным способом решить рассматриваемые проблемы.
Хотя первая версия данного калькулятора подражала алгоритму Су, разработанному в 2004 году, результаты, которые он производил, хотя и были свободными от зависти в математическом смысле, не всегда удовлетворяли людей на практике.
«Иногда у вас есть решения, которые удовлетворяют некоторой теоретической модели справедливости, но на практике справедливым вы интуитивно считаете другой расклад», — говорит руководитель проекта Ариэль Прокачча.
Он предлагает следующий пример. Представьте себе трехкомнатную квартиру, разделенную между тремя соседями. Арендная плата составляет 3 доллара. Первый житель заинтересован только в том, чтобы жить в первой комнате, второй интересуется только второй, а их сосед — третьей. Каждый человек согласен заплатить 3 доллара за свою комнату.
Одно из возможных решений заключалось бы в том, чтобы поместить каждого человека в комнату по его выбору и назначить всю сумму арендной платы первому жильцу. Второй и третий жильцы тогда заключат гораздо более выгодную сделку, но у первого соседа по дому нет причин возражать. Он платит 3 доллара — ровно столько, сколько он и хотел, ведь у него нет желания жить в другом месте дома.
«Это решение не должно вызвать зависти на уровне теории, но, очевидно, оно несправедливо», — говорит Прокачча. «Справедливо каждому поселиться в комнате, в которой он хочет жить, и платить 1 доллар».
Именно такого результата и пытается достичь алгоритм Spliddit. Во-первых, он пытается максимизировать разницу между тем, сколько житель готов заплатить за комнату, и тем, сколько он в конечном счете платит. Этот «излишек» показывает, насколько выгодна сделка для каждого жильца, и алгоритм гарантирует, что у каждого жильца в желаемой им комнате он будет выше, чем тот излишек, который у него был бы в другой комнате. Это удовлетворяет условию отсутствия зависти.
Но затем, пытаясь найти «интуитивно справедливое» решение, калькулятор находит комбинацию комнат, которые минимизируют разницу в излишках каждого жильца.
Короче говоря, алгоритм гарантирует, что каждый житель заключает выгодную сделку, которая не может быть намного выгоднее по сравнению с соседями.
С появлением Spliddit поменялся способ расчета тарифов на такси, кредитования, методики разделения задач. Одной из причин создания Spliddit было ознакомление широкой общественности с преимуществами математических методов решения проблем, связанных со справедливым разделением. Точно так же, как метод «Я разделяю, ты выбираешь», его алгоритм используется для урегулирования деловых конфликтов.
Создатель Spliddit надеется, что когда-нибудь компьютеры смогут находить решения в гораздо более сложных проблемах.