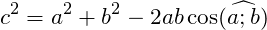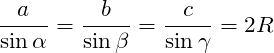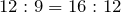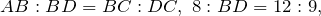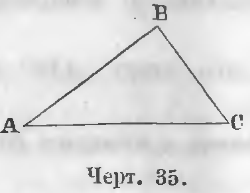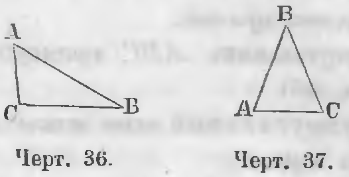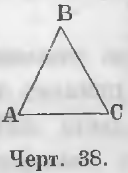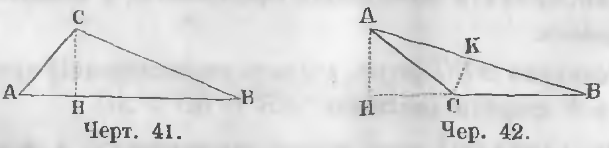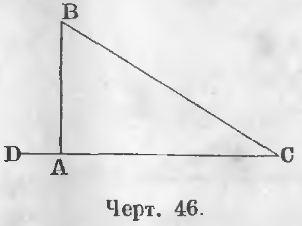как доказать что треугольник треугольный
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
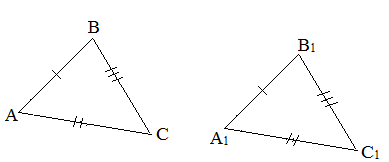
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
Существующие треугольники
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
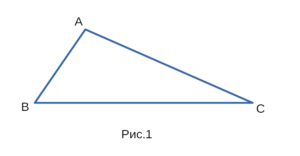
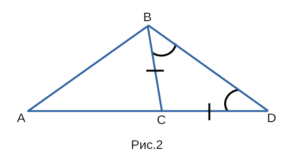
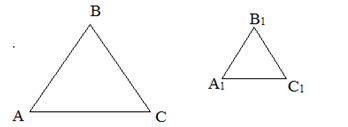
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
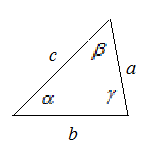
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
Геометрия
План урока:
Сумма углов треугольника
Рассмотрим произвольный треугольник АВС. Точки А, В и С не лежат на одной прямой, а потому через В можно провести прямую a, параллельную АС. При этом прямые СВ и АВ окажутся секущими для двух параллельных прямых:
Известно, что секущие образуют пары накрест лежащие углы, причем они равны. Отметим на рисунке эти пары и обозначим их как ∠1, ∠2, ∠3 и ∠ 4.
Равные углы (∠1 = ∠2, ∠3 = ∠4) отметим одним цветом. Также обозначим ∠АВС как ∠5:
С одной стороны, углы 2, 4 и 5 вместе образуют развернутый угол, то есть их сумма равна 180°:
В результате мы получили, что сумма углов треугольника АВС в точности равна 180°! В итоге мы можем сформулировать следующую теорему:
Задание. В треуг-ке один угол равен 50°, а второй – 60°. Чему равен третий угол этого треуг-ка?
Решение. Обозначим углы треугольника как ∠1, ∠2 и ∠3.
Получили обыкновенное уравнение с одной переменной. Для его решения просто перенесем слагаемые 50° и 60° из левой части в правую:
Задание. Докажите, что у любого треуг-ка есть хотя бы один угол, который не превосходит 60°.
Решение. Докажем это утверждение методом «от противного». Пусть существует такой треуг-к, у которого каждый из углов больше 60°. Это можно записать в виде трех неравенств:
В итоге имеем, что в сумме эти углы больше 180°, а это невозможно. Это противоречие, следовательно, треуг-к с тремя углами, каждый из которых больше 60°, не существует.
Задание. Основанием рав-бедр. ∆АВС является сторона АС. Известно, что ∠В = 40°. Чему равны ∠А и ∠С этого треуг-ка?
Решение. Сначала необходимо вспомнить важное свойство – углы равнобедренного треугольника при его основании равны друг другу. В нашем случае это значит, что ∠А = ∠С:
Задание. Один из углов при основании рав-бедр. треуг-ка равен 50°. Найдите два других угла.
Решение. Построим рисунок по условию задачи:
Отдельного внимания заслуживает равносторонний треуг-к. Напомним, что у него равны все три стороны. Построим его:
Теперь подумаем о том, чему равны его углы. С одной стороны, мы можем рассматривать ∆АВС как рав-бедр. с основанием АС, ведь AB = BC. Тогда∠А = ∠С. Но с другой стороны, всё тот же ∆АВС мы можем одновременно считать и рав-бедр. с основанием АВ, ведь АС = ВС. Из этого следует, что ∠А = ∠С. В итоге получаем, что все три угла ∆АВС равны:
Итак, получили удивительный факт – в равностороннем треуг-ке все углы равны 60°!
Рассмотрим чуть более сложную задачу, где неизвестен ни один из углов треуг-ка, однако известны некоторые соотношения между ними.
Задание. Первый угол треуг-ка больше второго в 2 раза, а третий равен сумме первых двух углов. Чему равны углы треуг-ка?
Решение. Для большей наглядности примем первый угол треуг-ка за неизвестную величину, то есть за х. Тогда второй угол будет равен 2х, а третий окажется равным их сумме:
Внешние углы треугольника
Построим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника:
На рисунке видно, что ∠ВСD является внешним. Но одновременно можно утверждать и ещё один факт – углы ∠АСВ и ∠ВСD являются смежными. Это позволяет нам дать следующее определение:
В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны.
Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С.
Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B:
Рассмотрим ещё несколько более тяжелых задач.
Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB.
Решение. Устно такую задачу не решить, поэтому построим рисунок:
АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ:
Отметим найденные углы на рисунке:
Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем. Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов:
Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию.
Решение. Выполним построение:
Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС.
Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть
В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК.
Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А.
Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство:
Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому
Сравнение сторон и углов треугольника
Докажем следующую теорему:
Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B:
Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком:
Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD.
Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что
Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ AC.
Задание. В ∆АВС известны углы:
Запишите стороны этого треуг-ка в порядке возрастания.
Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС
Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка:
Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно.
Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр.
Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса:
В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС).
Неравенство треугольника
Следующая важная теорема называется неравенством треугольника:
Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой:
Так как AD = АС + СD, то нам достаточно показать, что АВ
Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать.
Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других:
Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно.
Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием?
Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка.
Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется:
Треугольник
Определение треугольника
В любом треугольнике три угла и три стороны.
Против большего угла треугольника лежит большая сторона.
Виды треугольников
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
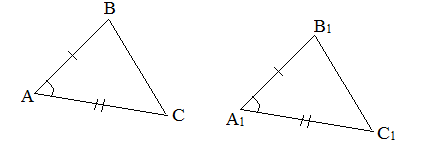
I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
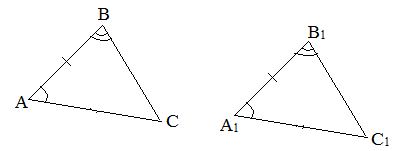
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
Треугольники называются подобными, если их стороны пропорциональны.
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.
Примеры решения задач
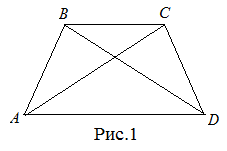
| Задание | Доказать, что в равнобокой трапеции диагонали равны. |
| Доказательство | В равнобокой трапеции  рассмотрим треугольники рассмотрим треугольники 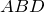 и и 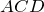 (рис. 1). Так как (рис. 1). Так как 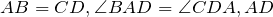 – общая сторона, то треугольники – общая сторона, то треугольники 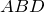 и и 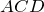 равны по первому признаку, а значит, равны все их элементы, т.е. равны по первому признаку, а значит, равны все их элементы, т.е. 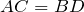 . . |
Что и требовалось доказать.
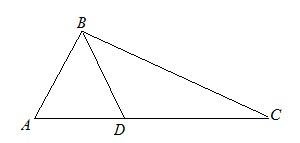
| Задание | В треугольнике 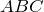 стороны стороны 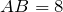 см см 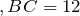 см см 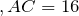 см. На стороне см. На стороне 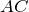 отмечена точка отмечена точка 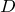 так, чтобы так, чтобы 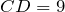 см. Найти отрезок см. Найти отрезок 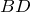 . . |
| Решение | Рассмотрим треугольники 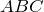 и и 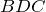 . Запишем отношение сторон . Запишем отношение сторон 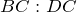 и и 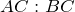 : : |
Так как выполняется равенство отношений, то соответствующие стороны треугольников пропорциональны, а также 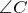
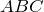
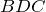
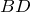
откуда 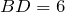
Математика
Треугольник есть определенная часть плоскости, ограниченная тремя взаимно пересекающимися прямыми линиями.
Стороны треугольника. Прямые линии, ограничивающие треугольник, называются сторонами треугольника.
Каждые две пересекающиеся прямые образуют угол треугольника.
Три пересекающиеся стороны образуют три угла треугольника.
Вершины. Точки пересечения сторон называются вершинами треугольника.
Треугольники получают различные названия, смотря по взаимному отношению его сторон и по углам, его составляющим.
Разделение треугольников по отношению к сторонам. По отношению к сторонам треугольники делятся на треугольники разносторонние, равнобедренные и равносторонние.
Разносторонний есть такой треугольник, у которого все стороны не равны.
Треугольник ABC (черт. 36) есть разносторонний треугольник. У него все стороны различны: AB > BC > AC.
Равнобедренный есть такой треугольник, у которого две стороны равны. На черт. 37 ABC есть равнобедренный треугольник. У него две стороны AB и BC равны (AB = BC).
Равносторонний есть такой треугольник, у которого все три стороны равны.
Треугольник ABC (черт. 38) равносторонний, ибо у него все стороны равны: AB = BC = AC.
Разделение треугольников по отношению к углам. По отношению к углам треугольники разделяются на остроугольные, прямоугольные и тупоугольные.
Остроугольный есть такой треугольник, у которого все три угла острые.
Треугольник ABC (черт. 39) есть остроугольный, ибо все его три угла A, B, C острые.
Прямоугольный есть такой треугольник, у которого один из углов прямой.
Треугольник ABC прямоугольный, ибо угол ABC прямой (черт. 40).
Тупоугольный есть такой треугольник, у которого один из углов тупой.
Треугольник ABC (черт. 36) тупоугольный, ибо угол ACB тупой.
В каждом треугольнике можно выбрать какую-нибудь сторону за основание, тогда перпендикуляр, опущенный из противоположной вершины на основание, называется высотою треугольника.
Высота есть расстояние вершины от основания треугольника, считаемое по перпендикуляру. Высота есть длина перпендикуляра, опущенного из вершины на основание.
Если на чертеже 41 примем линию AB за основание, то линия CH будет высотой треугольника. Если примем на чертеже 42 за основание линию BC, то высотой будет линия AH. Если бы за основание была выбрана линия AB, то высотой была бы линия CK.
Свойство сторон треугольника. Во всяком треугольнике каждая сторона меньше суммы и больше разности двух других сторон.
Так, в треугольнике ABC (черт. 35)
Равные треугольники. Два треугольника называются равными, если при наложении друг на друга они совмещаются всеми своими точками.
Равенство треугольников
Теорема 19. Два треугольника равны, если три стороны одного соответственно равны трем сторонам другого.
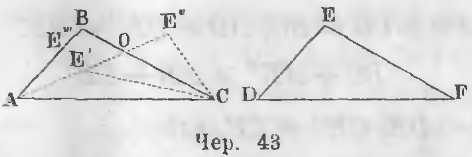
Дано. В двух треугольниках ABC и DEF (черт. 43) стороны равны
AB = DE, BC = EF, AC = DF
Требуется доказать, что ∆ ABC = ∆ DEF.
Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC точкой D на точку A. По равенству сторон AC и DF точка F упадет на точку C.
Чтобы доказать, что точка E упадет на точку B докажем, что она не может упасть ни внутри, ни вне, ни на одну из сторон треугольника.
a) Положим, что точка E упадет внутри треугольника в точку E’, тогда треугольник DEF примет положение треугольника AE’C, DE займет положение линии AE’ и EF положение линии E’C, следовательно,
Линия ABC, будучи внешней ломаной, больше линии AE’C внутренней ломаной, следовательно,
Заменяя AE’ и E’C равными им сторонами DE и EF, имеем:
но AB = DE, следовательно, BC > EF, что противоречит данным условиям. Итак, точка E не может упасть внутри треугольника.
b) Положим, точка E упала вне треугольника в точку E». В этом случае ∆AE»C = ∆DEF и тогда
Обозначим букой O точку пересечения линий AE» и BC. Из чертежа видно, что
AO + BO > AB
CO + OE» > E»C
Сложив эти неравенства, имеем:
AO + BO + CO + OE» > AB + E»C
Так как BO + CO = BC, AO + OE» = AE», то
Здесь AE» = DE, CE» = EF, следовательно,
Вычтя по равной величине из обоих частей последнего неравенства, получаем:
что противоречит данным условиям. Итак, точка E не может упасть вне треугольника.
c) Точка E не может упасть на одну из сторон треугольника в точку E»’, ибо стороны DC и AB равны. Точно также если бы E упала в точку O, то выходило бы, что BC > OC, но OC = EF, следовательно, BC > EF, что противоречит условию.
Итак, точка E должна непременно упасть в точку B, следовательно, при наложении сторона DE совпадет со стороной AB, а сторона EF со стороной BC и треугольник DEF с треугольником ABC.
Из равенства треугольников следует, что все остальные части их равны, т. е.
Теорема 20. Два треугольника равны, когда они имеют по равному углу, содержащемуся между равными сторонами.
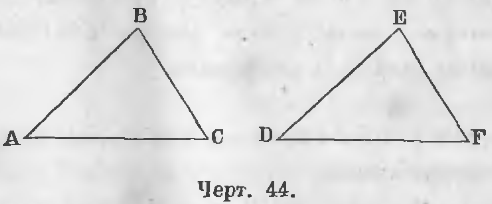
Дано. В двух треугольниках ABC и DEF (черт. 44)
AB = DE, AD = DF, ∠BAC = ∠EDF
Требуется доказать, что ∆ABC = ∆DEF.
Примечание. Иногда указывают равные части на чертеже, отмечая их одинаковыми значками.
Доказательство. Наложим треугольник DEF на треугольник ABC, сторону DF на сторону AC, точкой D на точку A; тогда по равенству линий DF и AC точка F упадет в точку C и по равенству углов A и D линия DE пойдет по линии AB; по равенству линий DE и AB точка E упадет на точку B. Если E и F две точки линии EF совпали с B и C двумя точками линии BC, то и вся линия EF совпадет с линией BC, и треугольник DEF совпадет с треугольником ABC. Отсюда следует, что и все остальные части треугольников равны, т. е.
Теорема 21. Два треугольника равны, если сторона и два лежащие на ней угла одного равны стороне и двум лежащим на ней углам другого треугольника.
Дано. В треугольниках ABC и DEF (черт. 44)
Требуется доказать, что ∆ABC = ∆DEF.
Доказательство. Наложим треугольник DEF на треугольник ABC, стороной DF на AC, точкой D на A, тогда по равенству сторон AC и DF точка F упадет на точку C. По равенству углов A и D линия DE пойдет по линии AB и по равенству углов C и F линия FE пойдет по линии CB. Так как линия FE и DE совпадут с линиями CB и AB, то и точка E непременно совпадет с точкой B, ибо две прямые линии пересекаются в одной точке, следовательно два треугольника равны (ЧТД).
Из того, что равные треугольники совмещаются при наложении всеми своими частями вытекает следствие. В равных треугольниках против равных сторон лежат равные углы и наоборот.
Соответственные части треугольников. В двух равных треугольниках равные углы и равные стороны называются соответственными углами и сторонами.
Внешний угол треугольника
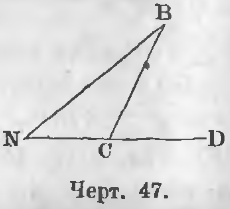
Внешний угол треугольника есть всякий угол смежный с углом треугольника.
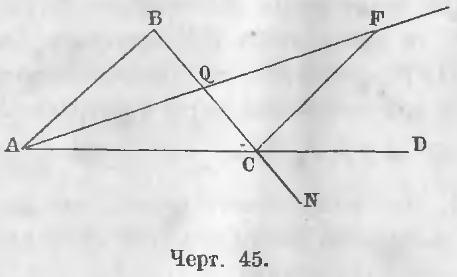
Так, на чертеже 45, угол BCD есть внешний угол.
Теорема 22. Во всяком треугольнике внешний угол больше каждого внутреннего не смежного с ним.
Дан внешний угол BCD (черт. 45).
Требуется доказать, что BCD > A и BCD > B.
Доказательство. Точку Q середину линии BC соединим с A и отложим на продолжении линии AQ линию QF равную AQ.
Соединим F с C; тогда два треугольника ABQ и QFC равны, ибо имеют по равному углу, лежащему между двумя равными сторонами.
Действительно, по построению BQ = QC, AQ = QF, а углы BQA и FQC равны как вертикальные, следовательно,
Если линия AQ = QF, то и ∠ABC = ∠BCF.
Угол BCD > угла BCF, следовательно, и угол BCD > ABC.
Производя подобное же построение, мы могли бы доказать, что угол ACN > угла BAC.
Так как ACN = BCD, то и угол BCD > угла BAC.
Прямоугольный треугольник
Следствие 1. В прямоугольном треугольнике из трех углов один прямой, а другие два острые.
Доказательство. Внешний угол BAD прямоугольного треугольника ABC (черт. 46) больше внутренних углов B и C, следовательно, оба угла B и C острые.
Гипотенуза. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой.
Катеты. Стороны прямоугольного треугольника, лежащие против острых углов, называются катетами.
Сторона BC есть гипотенуза, а стороны AB и AC катеты (черт. 46).
Гипотенуза больше каждого из катетов и меньше суммы двух катетов, ибо гипотенуза наклонная, а катеты перпендикулярны.
Тупоугольный треугольник
Следствие 2. В тупоугольном треугольнике один угол тупой, а два остальные угла острые.
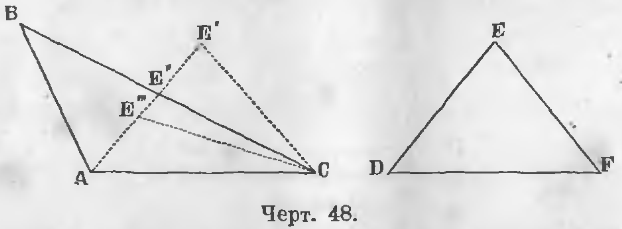
Дано. В двух треугольниках ABC и DEF (черт. 48)
AC = DF, AB = DE, угол BAC > угла EDF.
Требуется доказать, что BC > EF.
Так как D меньше угла A, то сторона DE пойдет по направлению AE’.
Здесь могут быть три случая: точка E может упасть вне, на сторону и внутри треугольника ABC, т. е. в точках E’, E» и E»’.
Не трудно заметить, что
AE» + E»B > AB
CE» + E»E’ > CE’
Сложив эти неравенства, получим:
AE» + E»B + CE» + E»E’ > AB + CE’
AE» + E»E = AE’
CE» + E»B = BC
Здесь AE’ = AB, следовательно,
BC > CE’ или
BC > EF (ЧТД).
BC > E»C, а следовательно, BC > EF.
По свойству ломаных (теорема 1)
AB + BC > AE»’ + E»’C или
AB + BC > DE + EF.
Так как AB = DE, то последнее неравенство дает
Итак во всех трех случаях BC > EF (ЧТД).
Дано. В треугольниках ABC и DEF (черт. 48) AB = DE, AC = DF и BC > EF.
Требуется доказать, что угол BAC > угла EDF.
1) Если бы угол BAC равнялся углу EDF, то два треугольника ABC и EDF были бы равны (теорема 20). В этом случае сторона BC равнялась бы стороне EF, что противоречит условию.
2) Если бы угол BAC был меньше угла EDF, то по предыдущей теореме и сторона BC была бы меньше EF, что также противоречит условию; следовательно, угол BAC больше угла EDF (ЧТД).
Взаимное отношение углов и сторон в треугольнике
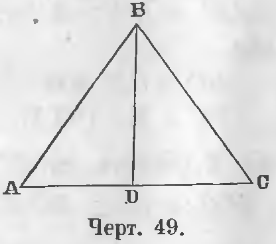
Дан равнобедренный треугольник ABC (черт. 49), т. е. треугольник, у которого AB = BC.
Требуется доказать, что ∠ A = ∠ C.
Два треугольника ABD и BDC равны, ибо имеют по три равных стороны. Действительно:
BD — общая сторона;
AD = DC по построению (D середина отрезка AC);
AB = BC по условию.
В равных треугольниках против равных сторон лежат равные углы, следовательно,
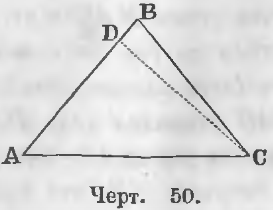
Дано. В треугольнике ABC ∠ A = ∠ C (черт. 50).
Требуется доказать, что AB = BC.
AC — общая сторона,
AD = BC по построению,
∠ A = ∠ C по условию.
Таким образом, AC и AD, две стороны треугольника ADC и уголь между ними A соответственно равны AC и BC, двум сторонам треугольника ABC, и углу C между ними. При этих условиях треугольники ADС и ABC были бы равны, что очевидно несообразно, ибо ∆ADC
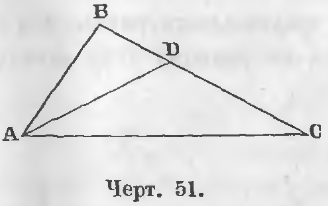
Дано. В треугольнике ABC (черт. 51) ∠ A > ∠ C.
Т ребуется доказать, что BC > AB.
В равнобедренном треугольнике ADC
следовательно, предыдущее неравенство примет вид
Дано. В треугольнике ABC (черт. 51) BC > AB.
Требуется доказать, что ∠ BAC = ∠ BCA.
b) Угол A не может быть меньше C, ибо тогда сторона BC была бы меньше AB (теорема 27), следовательно, BC > AB (ЧТД).
Равенство прямоугольных треугольников
Так как у прямоугольных треугольников прямые углы равны, то для равенства их требуется меньше условий.
Здесь имеют место два случая:
A) Когда два катета одного равны двум катетам другого и
Разберем эти два случая отдельно.
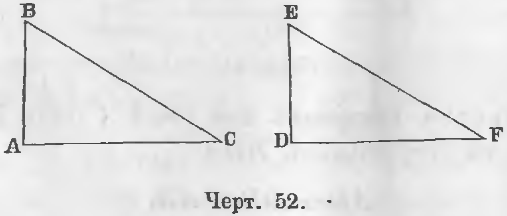
A) Прямоугольные треугольника ABC и DEF (черт. 52) имеют равные катеты
В этом случае треугольники равны, ибо они имеют по двум равным сторонам и по равному углу между ними.
B) Прямоугольные треугольники ABC и DEF имеют по равному катету и равной гипотенузе, следовательно, BC = EF, DE = AB (черт. 52).
Здесь тоже имеют место два случая:
Рассмотрим эти два случая отдельно:
A) Если прямоугольные треугольники имеют по равному катету и равному острому углу, то острый угол может быть a) прилежащий или b) противолежащий.
a) Прямоугольные треугольники имеют по равному катету и равному прилежащему острому углу, т. е.
DE = AB и ∠ E = ∠ B (черт. 52).
В этом случае треугольники равны, ибо они имеют по равной стороне и равным двум лежащим на ней углам.
b) Прямоугольные треугольники имеют по равному катету и по равному противоположному острому углу, т. е.
DE = AB, ∠ C = ∠ F (черт. 52).
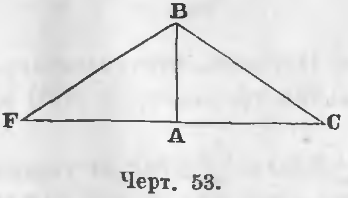
Повернуть треугольник DEF около оси DE и приставив сторону DE к стороне AB так, чтобы он занял положение ABF (черт. 53), получим равнобедренный треугольник FBC, ибо ∠ F = ∠ C, следовательно, наклонные BF и BC тоже равны и находятся на равных расстояниях AF и AC от перпендикуляра AB, т. е. два треугольника ABF и ABC равны, а следовательно равны и треугольники ABC и DEF (ЧТД).
B) Прямоугольные треугольники имеют по равной гипотенузе и равному острому углу, т. е.
BC = EF, ∠ C = ∠ F (черт. 52)
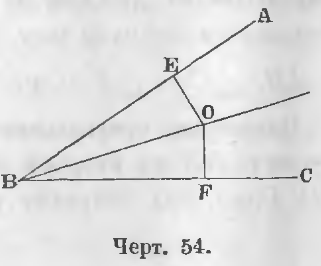
Дан угол ABC (черт. 54) и биссектриса BO, следовательно
Требуется доказать, что для какой-нибудь точки O перпендикуляры OE и OF равны.
∠ EBO = ∠ FBO по условию,
следовательно, EO = FO (см. теорему 30) (ЧТД).
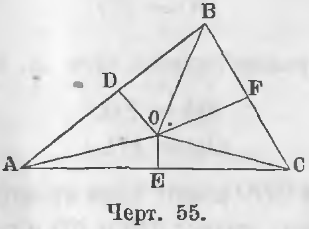
Дан треугольник ABC (черт. 55), O есть точка пересечения перпендикуляров DO и EO, восставленных из середин сторон AB и AC, следовательно,
Требуется доказать, что точка O находится на перпендикуляре, восставленном из середины третьей стороны BC.
Точка O находится на перпендикуляре восставленном из середины отрезка AC (теорема 17), следовательно, AO = CO.
Точка O находится на перпендикуляре, восставленном из середины отрезка AB, следовательно, AO = BO.
Откуда BO = CO, т. е. точка O находится на равном расстоянии от концов отрезка BC, следовательно, она находится на перпендикуляре FO, восставленном из середины отрезка BC (ЧТД).
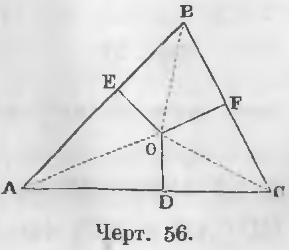
Даны линии AO и BO — биссектрисы углов A и B треугольника ABC и точка O (черт. 56) их точка пересечения, следовательно,
∠ BAO = ∠ CAO, ∠ ABO = ∠ CBO.
Требуется доказать, что линия OC будет тоже биссектрисой угла C.
Из того, что AO биссектриса угла A, следует (теорема 31), что
Из того, что BO биссектриса угла B, следует, что
Треугольники CFO и CDO равны, как прямоугольные треугольники, имеющие по равному катету DO и FO и гипотенузе CO (теорема 29), откуда
Следовательно, прямая CO есть биссектриса угла BCA (ЧТД).