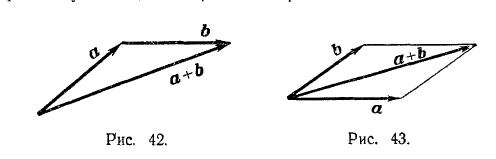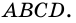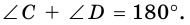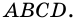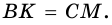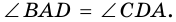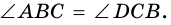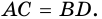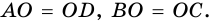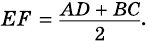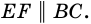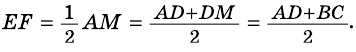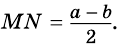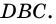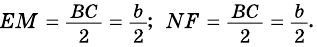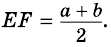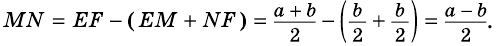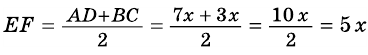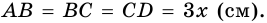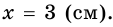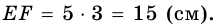как доказать что точки являются вершинами трапеции
Как доказать что точки являются вершинами трапеции
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
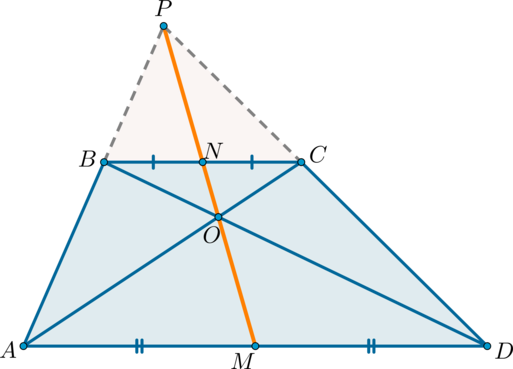
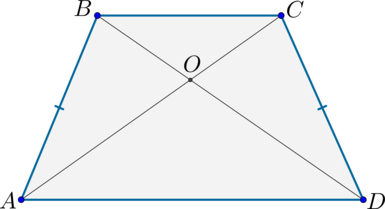
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
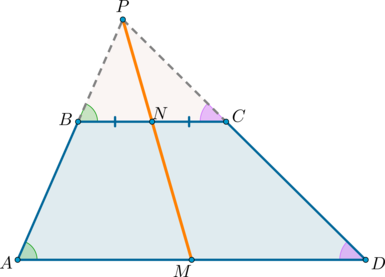
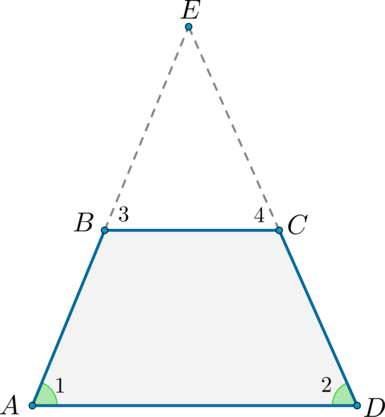
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
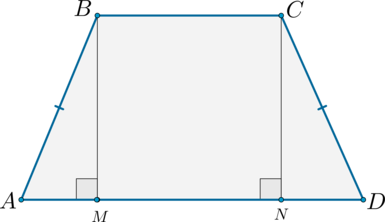
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
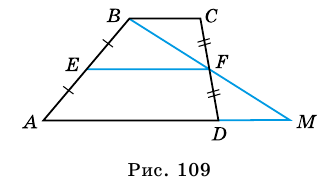
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
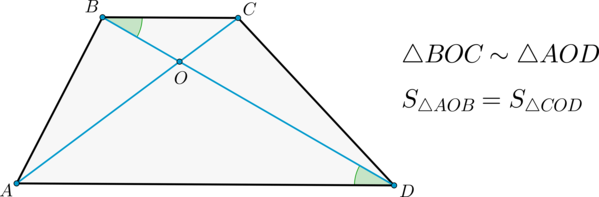
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
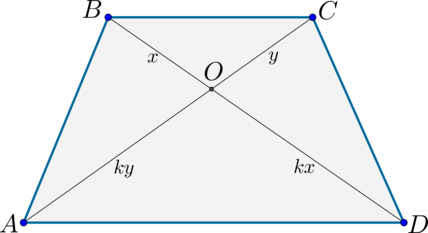
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
Трапеция
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
Определение
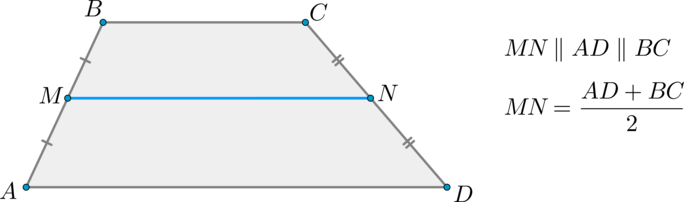
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
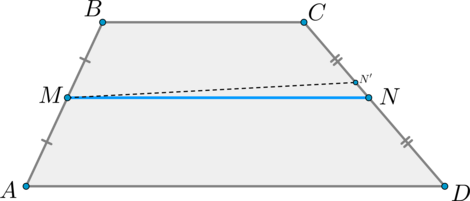
1) Докажем параллельность.
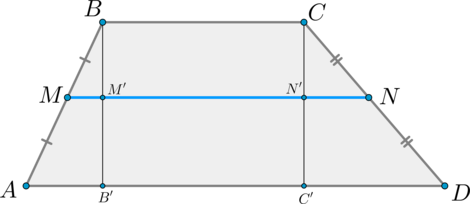
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
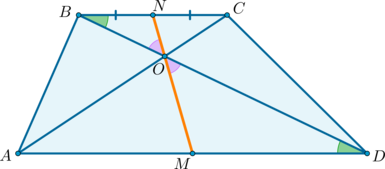
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
\(\triangle BNO\sim \triangle DMO\) по двум углам ( \(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
2)
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Доказать что точки служат вершинами трапеции
1. Проверить, что точки служат вершинами трапеции. Найти длины её параллельных сторон.
A(3;-1;2)
B(1;2;-1)
C(-1;1;-3)
D(3;-5;3)
2. Доказать, что точки лежат на одной прямой, причём точка B расположена между A и С. Составить канонические уравнения этой прямой.
A(-3;-7;-5)
B(0;-1;-2)
C(2;3;0)
AB: `(x+3)/3=(y+7)/6=(z+5)/3`
BC: `x/2=(y+1)/4=(z+2)/2`
AC: `(x+3)/5=(y+7)/10=(z+5)/5`
Вообщем подставляю 3 точку в уравнение, получаю верное равенство => все 3 точки лежат на 1 прямой.
Как доказать, что B лежит между A и C?
Если вам понравился ответ, не забудьте нажать кнопку Спасибо, Отметить мой ответ, как лучший и поставить 5 звезд!
Суммой а + b двух векторов а и b называется вектор, который идет из начала вектора а в конец вектора b при условии, что вектор b приложен к концу вектора а (правило треугольника) Построение суммы а + b изображено на рис. 42.
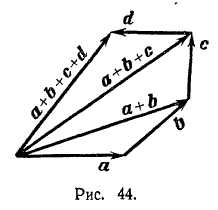
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 44, где изображено построение суммы четырех векторов а, b, с, d).
Произведением ом (или также aα) вектора а на число α называется вектор, модуль которого равен произведению модуля вектора а на модуль числа α; он параллелен вектору а или лежит с ним на одной прямой и направлен так же, как вектор а, если α — число положительное, и противоположно вектору а, если α — число отрицательное.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Имеют место следующие две основные теоремы о проекциях векторов:
1. Проекция суммы векторов на какую-нибудь ось равна сумме их проекций на эту же ось:
2. При умножении вектора на число его проекция умножается «а то же число:
Если а = (X; Y; Z), то для любого числа α
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
является пропорциональность их координат:
Тройка векторов i, j, k называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
1) вектор i лежит на оси Ох, вектор i — на оси Оу, вектор k — на оси Oz;
2) каждый из векторов i, j, k направлен на своей оси в положительную сторону;
3) векторы i, j, k — единичные, т. е. |i| = 1, |j| = 1, |k| = 1
Каким бы ни был вектор а, он всегда может быть разложен по базису i, j, k, т. е. может быть представлен в виде:
коэффициенты этого разложения являются координатами вектора а (т. е. X, Y, Z суть проекции вектора а на координатные оси).
762. Даны: |а| = 13, |b| = 19 и |а + b| = 24. Вычислить |а — b|.
763. Даны: |а| = 11, |b| = 23 и |а — b| = 30. Определить |а + b|.
764. Векторы а и b взаимно перпендикулярны, причем |а| = 5 и |b| = 12. Определить |a + b| и |а — b|.
765. Векторы а и b образуют угол φ = 60°, причем |а| = 5 и |b| = 8. Определить |а + b| и |а — b|.
766. Векторы а и b образуют угол φ = 120°, причем |а| = 3 и |6| =5. Определить |a + b| и |а — b|.
771. Точка О является _центром тяжести треуголь-ника АБС. Доказать, что OA + OB + OC = 0.
772. В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его сторонами: АB = m, BC = n, CD = р, DE = q и EA = r. Построить векторы: 1) m — n + p — q + r; 2)m + 2р + 1/2r; 3) 2m + 1/2n — Зр — q + 2r.
1) m + n + р; 2) m + n + 1/2p;
3) 1/2m + 1/2n + р; 4) m + n — р;
774. Три силы М, N и Р, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей R, если известно, что |М| = 2кГ, |N| = 10 кГ и |Р| = 11 кГ.
777. Определить, при каких значениях α, β векторы а = 2i + 3j + βk и b = ai — 6j + 2k коллинеарны.
783. Дано разложение вектора с по базису i, j, k: с = 16i — 15j + 12k. Определить разложение по этому же базису вектора d, параллельного вектору с и противоположного с ним направления, при условии, что |d| = 75.
784. Два вектора а = и b = приложены к одной точке. Определить координаты вектора с, направленного по биссектрисе угла между векторами а и b, при условии, что |с| = 3√42.
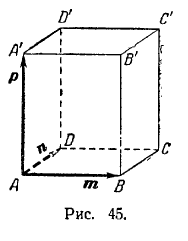
785. Векторы АB = и АC = совпадают со сторонами треугольника ABC. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами AM, BN, СР.
786*). Доказать, что если р и q — какие угодно не- коллинеарные векторы, то всякий вектор, лежащий в их плоскости, может быть представлен в виде: a = αp + αq.
Доказать, что числа α и β векторами а, р и q определяются однозначно. (Представление вектора а в виде a = αp + βq называется разложением его по базису р, q; числа α и β называются коэффициентами этого разложения.)
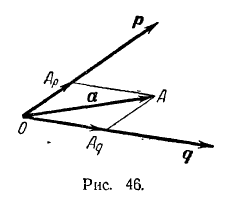
Доказательство. Приведем векторы а, р и q к общему началу, которое обозначим буквой О (рис. 46). Конец вектора а обозначим буквой А. Через точку А проведем прямую, параллельную вектору q. Точку пересечения этой прямой с линией действия вектора р обозначим через Аp. Аналогично, проводя через точку А прямую, параллельную вектору р, получим в пересечении с линией действия вектора q точку Aq.
По правилу параллелограмма получим:
Так как векторы OA p и р лежат на одной прямой, то вектор OA p может быть получен умножением вектора р на некоторое число α
Из равенств (1). (2) и (3) получаем: а = αр + βq. Тем самым возможность требуемого разложения доказана. Остается доказать, что коэффициенты α и β этого разложения определяются однозначно.
*) Задачи 786 и 792 существенны для правильного понимания остальных задач. Решение первой из них здесь приводится полностью.
Предположил, что вектор а имеет два разложения;
а = αр + βq, а = α’р + βq,
и, например, α’ ≠ α. Вычитая почленно одно из другого, получаем:
(α’ — α)р + (β’ — β)q = 0 или р = (β — β’)/(α’ — α)q.
Но это равенство означает коллинеарность векторов р и q, которые, однако, по условию являются неколлинеарными. Следовательно, неравенство α’ ≠ α невозможно. Аналогично доказывается, что невозможно неравенство β’ ≠ β. Таким образом,α’= α, β’ = β,т. е. двух различных разложений один и тот же вектор иметь не может.
790. Принимая в качестве базиса векторы AB = b и AC = с, совпадающие со сторонами треугольника ABC, определите разложение векторов, приложенных в вершинах треугольника и совпадающих с его медианами.
792. Доказать, что если р, q и r — какие угодно некомпланарные векторы ), то всякий вектор а пространства может быть представлен в виде: а = αр + βq + γr. Доказать, что числа α, β, γ векторами а, р, q и r определяются одйозначно. (Представление вектора а в виде a = αр + βq + γr называется разложением его по базису р, q, r. Числа α, β и γ называются коэффициентами этого разложения.)
*) Три вектора называются некомпланарными, если после приведения к общему началу они не лежат в одной плоскости.
Трапеция и ее свойства с определением и примерами решения
Содержание:
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
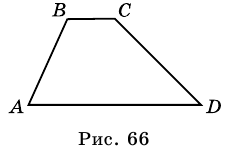
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 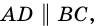
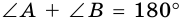
2. Трапеция является выпуклым четырехугольником.
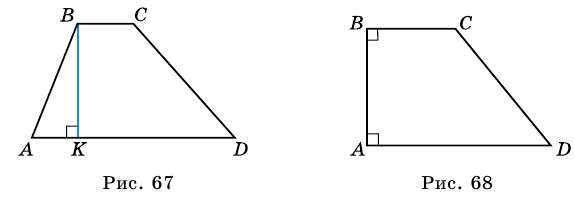
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 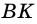
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 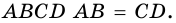
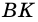
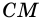
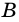
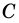
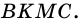
2) 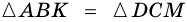
3) Также 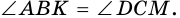
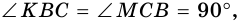
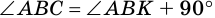
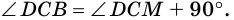
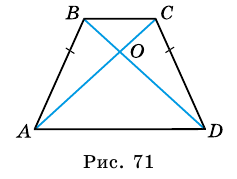
2. Диагонали равнобокой трапеции равны.
Доказательство:
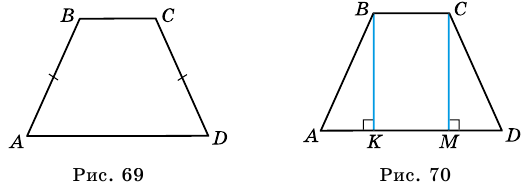
Рассмотрим рисунок 71. 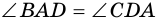
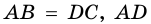
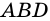
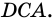
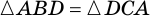
Пример:
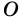
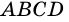
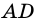
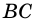
Доказательство:
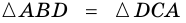
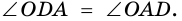
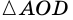
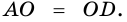
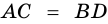
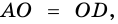
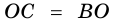
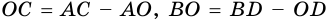
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 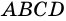
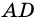
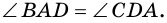
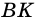
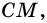
2) Тогда 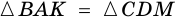
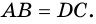
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 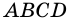
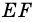
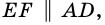
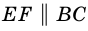
1) Проведем луч 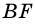
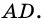
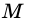
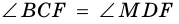
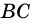
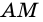
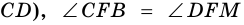
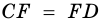
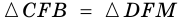
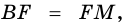
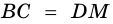
2) Поскольку 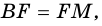
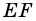
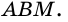
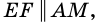
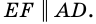
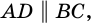
3) Кроме того,
Пример:
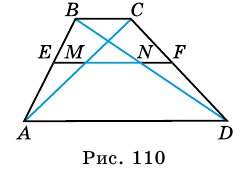
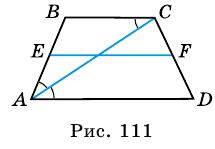
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 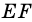
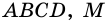
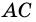
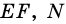
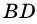
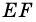
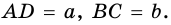
1) Так как 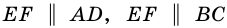
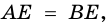
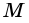
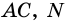
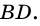
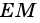
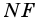
Тогда
2) 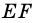
3)
Пример:
Решение:
Пусть 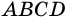
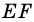
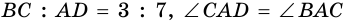
1) Обозначим 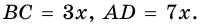
2) 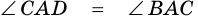
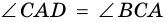
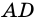
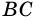
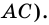
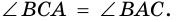
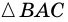
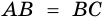
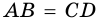
3) Учитывая, что 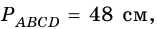
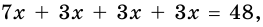
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.