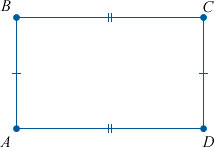
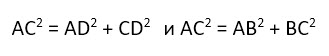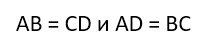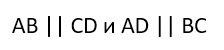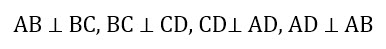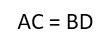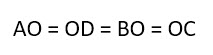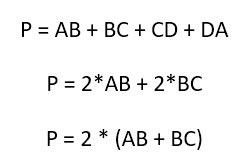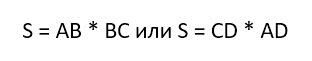как доказать что прямоугольник квадрат
Является ли квадрат прямоугольником
Знания о простых геометрических фигурах мы получаем еще в дошкольном возрасте.
Задача школьной программы углубить и расширить эти знания.
Но довольно часто у родителей возникает вопрос к учителям начальных классов по определению математически понятий квадрата и прямоугольника.
Некоторые учителя дают знания о том, что квадрат и прямоугольник две разные фигуры. Квадратом может называться фигура только с равными сторонами. У прямоугольника одна сторона должна быть длиннее. Объясняют это тем, что детям рано понимать сложные формы и доказательства теорем. Достаточно знаний, о том, что это две разные фигуры. Знать о том, что фигура геометрическая фигура квадрат это частный случай прямоугольника в этом возрасте не обязательно.
Квадрат и прямоугольник — четырёхугольники
И квадрат, и прямоугольник относят к типу геометрических фигур четырёхугольников. Четырёхугольником может быть и фигура, у которой ни углы, ни стороны по длине не совпадают.
Квадрат представляет собой четырёхугольную геометрическую фигуру с равными сторонами и углами, стороны которой параллельны друг другу. Квадрат, не являющийся прямоугольником, не будет являться квадратом по определению.
Признаки квадрата
1. Если противолежащие и смежные стороны данного прямоугольника равны, то такой прямоугольник является квадратом.
2. Диагонали квадрата всегда перпендикулярны друг другу
3. Ромб будет называться квадратом, если один угол его равен 90 градусам.
Прямоугольник это многоугольная геометрическая фигура, у которой есть четыре вершины и соответственно, четыре стороны как одной, так и разной длины. Иначе говоря, это многоугольник с четырьмя углами.
Признаки прямоугольника
1. Если у фигуры есть три прямых угла это прямоугольник.
2. Равные диагонали в параллелограмме указывают на то, что перед нами прямоугольник.
3. Фигура будет прямоугольником, если перед нами параллелограмм с одним прямым углом.
4. Противолежащие стороны у прямоугольника равны.
Любой квадрат является прямоугольником
Что общего у квадрата и прямоугольника
2. Равные по длине диагонали.
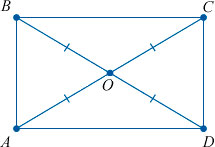
3. Точка пересечения диагоналей делит их пополам.
4. Противолежащие стороны равны.
Два основных отличия квадрата от прямоугольника
1. У квадрата равны все четыре стороны.
2. У прямоугольника равны противолежащие стороны, которые параллельны. Таким образом, квадрат прямоугольник с равными сторонами. Любой квадрат будет одновременно и прямоугольником, но не каждый прямоугольник является квадратом.
Существует квадрат, который не является прямоугольником
Прямоугольник и квадрат
Определение
Прямоугольник – это параллелограмм, у которого один угол прямой.
Таким образом, прямоугольник обладает всеми свойствами параллелограмма:
\(\sim\) противоположные стороны попарно равны;
\(\sim\) диагонали точкой пересечения делятся пополам.
Теоремы: свойства прямоугольника
1) Все углы прямоугольника прямые.
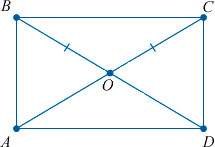
2) Диагонали прямоугольника равны.
Доказательство
Следствие
Теоремы: признаки прямоугольника
1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
2) Если в выпуклом четырехугольнике все углы прямые, то он – прямоугольник.
Доказательство
1) Пусть в параллелограмме \(ABCD\) диагонали равны.
2) Рассмотрим четырехугольник \(ABCD\) :
Определение
Два эквивалентных определения квадрата:
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат – это ромб, у которого один угол прямой.
Свойства квадрата
Так как квадрат является прямоугольником и ромбом, то он обладает всеми свойствами прямоугольника и ромба:
\(\sim\) Все углы квадрата равны \(90^\circ\) ;
\(\sim\) Все стороны квадрата равны;
\(\sim\) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это.
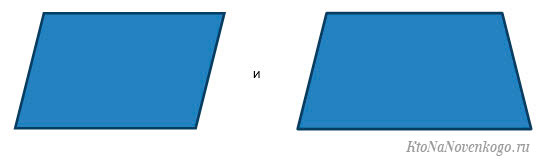
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
Диагонали прямоугольника
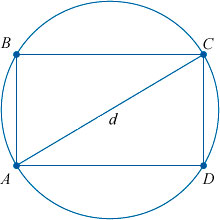
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
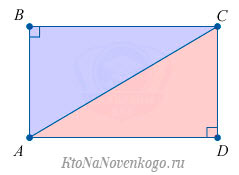
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
Квадрат, его свойства и признаки.
Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
Квадратом называется параллелограмм, у которого все стороны и углы равны.
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
У квадрата диагонали взаимно перпендикулярны.
У квадрата диагонали являются биссектрисами его углов.
У квадрата диагонали равны.
У квадрата стороны являются высотами.
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА ( I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Так как – прямоугольник, то у него противолежащие стороны равны.
– квадрат (по определению), ч.т.д.
ТЕОРЕМА ( II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).
ТЕОРЕМА ( III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
ТЕОРЕМА ( IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
ТЕОРЕМА ( V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
ТЕОРЕМА ( VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.
ТЕОРЕМА ( VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
1. Так как , то четырёхугольник является ромбом (по V признаку ромба).
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
Если в ромбе диагонали равны, то этот ромб является квадратом.
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.
В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
Найдите периметр квадрата по данным на рисунке.
Прямоугольник
Частным видом параллелограмма является прямоугольник.
| Прямоугольником называют параллелограмм, у которого все углы прямые |
Особое свойство прямоугольника
Доказательство
Доказать: AC = DB
Доказательство:
Теорема
Доказательство
Доказательство:
Рассмотрим 

Теорема
Доказательство
Доказательство:
Противолежащие углы параллелограмма равны, 



Две теоремы, доказанные выше, называют признаками прямоугольника.
Поделись с друзьями в социальных сетях: