Существуют такие системы отсчета относительно которых тела сохраняют свою скорость неизменной если

ГДЗ конспекты по физике 9 класс Задание: Законы Ньютона

I закон Ньютона (Закон инерции)

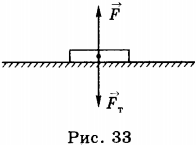
Существуют такие системы отсчёта, относительно которых тела сохраняют свою скорость неизменной (по модулю и направлению), если на них не действуют другие тела или действия других тел компенсируются.

Инерциальные системы отсчёта – те, в которых закон инерции выполняется.

Если V = const, то \(\overrightarrow\) = 0 («не пнёшь, – не полетит»).

II закон Ньютона

Ускорение тела прямо пропорционально равнодействующей силе, приложенной к телу, и обратно пропорционально его массе.

F – сила | \(\frac<кг\ м><с^<2>>\) = Н («как пнёшь, так и полетит»).

Особенности:

вектор силы и вектор ускорения сонаправлены;

справедлив для любых сил;

справедлив для тел, движущихся со скоростями много меньше скорости света.

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Источник

Об извращённом толковании Первого закона Ньютона в современной физике

В начале ХХ века в физике появились умники-недоучки, не признающие саму методологию научного творчества и объявившие о неких «ограничениях», сужающих область применимости механики Ньютона (I. Newton).

Начнём с того, как трактуются законы Ньютона в современных учебниках по физике. Например, в книге А.В. Перышкина и Е.М. Гутника [1] на стр.42 написано следующее:

с точки зрения современных представлений первый закон Ньютона формулируется так:

существуют такие системы отсчёта, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.

Всякое тело продолжает удерживаться в состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.

Т.е., Ньютон рассматривал вопрос о системах отсчёта очень скрупулёзно и сумел абстрагироваться от кажущихся (относительных) движений, мешающих понять первопричину всех движений и изменения движений – действие силы.

В этом умении абстрагироваться от, искажающих суть, факторов и заключается гениальность Ньютона и его предшественников – коперниканцев, отвергнувших теорию движения планет Птолемея (Πτολεμαΐος), основанную только на описании относительных, кажущихся движений, и, именно поэтому, бессильной в определении причин, приводящих к таким движениям. Получается, что «поправляющие» Ньютона пытаются отбросить нас в эпоху Птолемея и Аристотеля (Αριστοτέλης)…

Кстати, вся теория относительности Эйнштейна рассматривает именно относительные, кажущиеся движения и неудивительно, что следствиями этой теории являются неразрешимые парадоксы.

Также следует отметить, что в теории Эйнштейна абсолютизируется состояние покоя, что, опять же, является возвратом к временам Аристотеля и Птолемея. А Ньютон, своим Первым законом, специально подчёркивает, что v = 0 = const не имеет никаких преимуществ по сравнению с v = const > 0.

Включение в формулировку Первого закона инерциальной системы отсчёта неприемлемо и в том смысле, что физический закон реализуется независимо от того – наблюдаем мы за процессом или нет, измеряем что-либо или нет… Тем более, что определение инерциальной системы отсчёта дают через Первый закон Ньютона (см., например, на стр.13 в [3]), а потом переформулируют этот же закон, используя понятие «инерциальной системы отсчёта»… Очень «научный» подход…

Итак, одна из главных идей Первого закона Ньютона заключается в том, что «состояние покоя» не является особым случаем, а как раз наоборот, это – частный случай «состояния прямолинейного равномерного движения», когда скорость равна нулю, т.е. любое другое число, равноправно во всех отношениях с нулём!

Второй важный момент. Утверждают, что Ньютон «искал» какую-то абсолютную точку отсчёта и, в конце концов, «закончил» эти поиски в центре Солнца. Как бы то ни было, но Первый закон, как раз, отрицает абсолютность нулевой скорости, а, следовательно, и абсолютность какой-либо точки отсчёта… Вполне возможно, что эти «поиски» (если они, на самом деле, были…) – другое проявление самого Ньютона, не как физика, а как теолога. Ведь, само утверждение «существуют такие системы отсчёта» в корне неверно! При точных измерениях мы всегда обнаружим ускорения. Даже корабль, двигающийся с постоянной скоростью при полном штиле не является инерциальной системой отсчёта, потому что Земля шарообразная и корабль движется по кривой поверхности моря, не говоря уже о том, что сама Земля вращается…

И ещё. Что бы ни говорили «квантомеханики»: нет ни одного эксперимента, показывающего, что в микромире этот закон не выполняется. Наоборот, то же Броуновское движение доказывает «дословное» (т.е. без дополнительных пояснений) выполнение закона: микрочастица движется от одного столкновения до другого по прямой и с постоянной скоростью.

Т.е., утверждая выше об отсутствии инерциальных систем отсчёта я немного погорячился? В микромире они существуют? Похоже на то!

Но, в то же время в микромире отсутствуют… ускорения (!), потому что там нет «полей» как в макромире и все взаимодействия происходят только посредством «столкновений» в очень малой области пространства за очень короткое время… Для подтверждения этого тезиса сошлюсь на авторитет Ричарда Фейнмана (Richard Feynman), утверждавшего в [4]:

Хочу особенно подчеркнуть, что свет существует именно в виде частиц – это очень важно знать. Это особенно важно знать тем из вас, кто ходил в школу, где, возможно, что-то говорили о волновой природе света. Я говорю вам, как он на самом деле ведёт себя – как частицы

Кстати, сами фейнмановские диаграммы изначально строились как «траектории» частиц до и после взаимодействия в одной пространственной и одной временной осях координат, но потом «увлеклись» математикой и об этом «забыли», опять же, потому что решили «ограничить» применимость Законов Ньютона…

Источник

Законы Ньютона

1. В основе классической механики лежат три закона Ньютона, которые были сформулированы им при обобщении результатов наблюдений и опытов в конце XVII в.

Первый закон, включённый Ньютоном в систему законов, был открыт Галилеем и назван им законом инерции. Закон инерции формулируется следующим образом: если на тело не действуют другие тела, то оно либо находится в покое, либо движется равномерно прямолинейно.

2. В природе не существует отдельных изолированных тел. Любое тело взаимодействует с окружающими телами. Несмотря на это, взаимодействующие тела могут находиться в покое или двигаться равномерно и прямолинейно.

3. При компенсации действия на тело других тел оно может двигаться равномерно прямолинейно.

Например, если по прямой горизонтальной дороге движется автомобиль, то при компенсации действия на него силы тяги двигателя и силы трения со стороны поверхности дороги движение автомобиля будет равномерным.

Можно утверждать, что тело сохраняет состояние покоя, если действие на него других тел скомпенсировано.

Явление сохранения скорости тела постоянной (в том числе и равной нулю) называют явлением инерции.

4. Тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела или действие других тел скомпенсировано не во всех системах отсчёта, а только в инерциальных системах отсчёта.

Инерциальными системами отсчёта называются такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия других тел компенсируются. Инерциальной можно считать систему отсчёта, связанную с Землёй. Системы отсчёта, движущиеся относительно Земли равномерно и прямолинейно, также являются инерциальными.

Системы отсчёта, движущиеся с ускорением относительно инерциальной системы отсчёта, например относительно Земли, называют неинерциальными.

5. Значение первого закона Ньютона состоит в том, что он устанавливает существование инерциальных систем отсчёта (таких систем отсчёта, относительно которых тела движутся с постоянной скоростью при компенсации внешних воздействий). Именно для таких систем отсчёта справедливы все другие законы Ньютона.

6. Второй закон Ньютона устанавливает зависимость ускорения одного из взаимодействующих тел от его массы и действующей на него силы. Наблюдения и опыты свидетельствуют о том, что чем больше сила, действующая на тело, тем больше ускорение, которое оно приобретает. Так, чем сильнее водитель нажимает на педаль тормоза, тем
больше сила и тем быстрее автомобиль остановится. Значит, чем больше действующая на автомобиль сила сопротивления, тем больше его ускорение.

Ускорение, которое приобретают тела под действием одинаковой силы, зависит от массы тел. Например, грузовому автомобилю требуется большее время, чем легковому, для того, чтобы, имея некоторую одинаковую скорость, остановиться, выключив двигатель. Из этого примера следует, что чем больше масса тела, тем меньшее ускорение оно получает под действием некоторой постоянной силы.

7. Второй закон Ньютона формулируется следующим образом: ускорение, с которым движется тело прямо пропорционально действующей на тело силе и обратно пропорционально массе тела.

Записанное равенство представляет собой второй закон Ньютона.

В механике Ньютона ускорение тел обусловлено только их взаимодействием. Следовательно, второй закон Ньютона справедлив в инерциальных системах отсчёта.

8. Действие тел друг на друга носит взаимный характер, т.е. в результате взаимодействия
каждое тело приобретает ускорение, и, следовательно, на каждое из взаимодействующих тел действует сила. Например, груз, висящий на нити, действует на нить с силой, направленной вертикально вниз \( (\vec_1) \) ​, и растягивает её (рис. 34). В свою очередь, нить действует на груз с силой, направленной вертикально вверх \( (\vec_2) \) ​.

9. Измерения показывают, что:

10. Из соотношения следует: ​ \( m_1a_1=m_2a_2 \) ​.

Поскольку ускорение — величина векторная и ускорения, которые получают тела, направлены в противоположные стороны, то ​ \( m_1\vec_1=-m_2\vec_2 \) ​.

Это равенство и выражает третий закон Ньютона.

Третий закон Ньютона формулируется следующим образом: тела действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны. Эти силы направлены вдоль прямой, соединяющей взаимодействующие тела (материальные точки).

Третий закон Ньютона говорит о том, что силы всегда проявляются парами.

Эти силы часто называют силами действия и противодействия. При этом безразлично, какую из двух сил назвать силой действия, а какую — силой противодействия.

Эти силы приложены к разным телам, и их нельзя складывать, т.е. нельзя сказать, что силы действия и противодействия уравновешивают друг друга.

Силы, с которыми взаимодействуют тела, всегда одной природы.

Третий закон Ньютона, так же как первый и второй законы, справедлив в инерциальных системах отсчёта.

10. При переходе от одной инерциальной системы отсчёта к другой не изменяются ни ускорение, ни масса тала, ни действующая на него сила. Следовательно, можно утверждать, что законы механики одинаковы для всех инерциальных систем отсчёта, или, что то же самое, все механические явления протекают одинаково во всех инерциальных системах отсчёта при одинаковых начальных условиях. Это утверждение называется принципом относительности Галилея.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Утверждение, что материальная точка покоится или движется равномерно прямолинейно, если на неё не действуют другие тела или действие на неё других тел взаимно уравновешено,

1) неверно ни для каких систем отсчёта
2) верно для инерциальных систем отсчёта
3) верно для неинерциальных систем отсчёта
4) верно при любых условиях

2. Система отсчёта, связанная с Землёй, может считаться инерциальной. Система отсчёта, связанная с автобусом, тоже будет инерциальной, если он

1) движется равномерно по извилистой дороге
2) тормозит у остановки
3) отъезжает от светофора
4) движется равномерно по прямолинейному участку пути

3. В каком из приведённых примеров тело движется по инерции:

1) равномерно движущийся по горизонтальной дороге автомобиль
2) автомобиль, движущийся по горизонтальной дороге с выключенным двигателем
3) автомобиль, поворачивающий направо
4) автомобиль, выезжающий со стоянки

4. Яблоко, лежащее неподвижно на столе вагона движущегося поезда покатился вправо, если смотреть по ходу поезда. Как изменилось движение поезда?

1) скорость поезда увеличилась
2) скорость поезда уменьшилась
3) поезд повернул влево
4) поезд повернул вправо

5. Можно ли считать инерциальной системой отсчёта движущийся автомобиль?

1) можно всегда
2) можно, только если он движется равномерно и прямолинейно
3) можно только во время разгона и торможения
4) нельзя ни при каких условиях

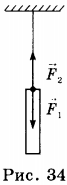
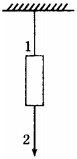
6. Массивный груз подвешен на тонкой нити 1. К грузу прикреплена такая же нить 2. Если
медленно тянуть за нить 2, то оборвётся

1) только нить 1
2) только нить 2
3) нить 1 и нить 2 одновременно
4) либо нить 1, либо нить 2, в зависимости от массы груза

7. Нить, привязанная одним концом к вбитому в стену гвоздю, разорвётся, если другой её конец тянуть с силой не менее 50 Н. Чему равно наименьшее значение сил, с которыми растягивают эту же нить за оба конца, при котором она рвётся?

1) 25 Н
2) 50 Н
3) 75 Н
4) 100 Н

8. Два ученика тянут динамометр в противоположные стороны с силой 60 Н каждый. Каково показание динамометра?

1) 0 Н
2) 30 Н
3) 60 Н
4) 120 Н

1) ​ \( F_2 = 0 \) ​
2) ​ \( F_1=F_2 \) ​
3) \( F_1>F_2 \)
4) \( F_1

1) 1,5 т
2) 7,5 т
3) 15 т
4) 75 т

11. Из приведенных утверждений выберите два правильных и запишите их номера в таблицу.

1) законы Ньютона справедливы во всех системах отсчета
2) первый закон Ньютона утверждает существование инерциальных систем отсчета
3) равнодействующая сил действия и противодействия равна нулю
4) силы действия и противодействия имеют одинаковую природу
5) второй закон Ньютона говорит о том, что масса тела прямо пропорциональна действующей на тело силе

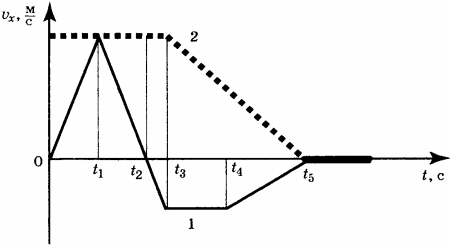
12. Два тела движутся по оси ​ \( Ox \) ​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​ \( t_3-t_5 \) ​ на тело 2 действует постоянная сила.
2) В промежутке времени ​ \( 0-t_3 \) ​ сила сообщает телу 1 положительное ускорение
3) В промежутке времени ​ \( t_4-t_5 \) ​ на тело 1 сила не действует
4) Модуль силы, действующей на тело 1 в промежутки времени ​ \( 0-t_1 \) ​, ​ \( t_1-t_2 \) ​ различен.
5) В промежутке времени ​ \( t_1-t_2 \) ​ сила сообщает телу 1 отрицательное ускорение

Часть 2

13. Тело массой 7 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 4 с груз был поднят на высоту 16 м?

Источник

Существуют такие системы отсчёта, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел скомпенсированы.

Системы отсчёта, в которых выполняется первый закон Ньютона (закон инерции), называют инерциальными системами отсчёта (ИСО). Такой системой отсчёта является Земля, а также системы отсчёта, которые относительно Земли покоятся или движутся прямолинейно и равномерно. Таких систем бесконечное множество. Во всех инерциальных системах отсчёта причиной изменения скорости тел является взаимодействие тел. Действие одного тела на другое характеризуют силой ( . Сила характеризуется: 1) точкой приложения; 2) направлением; 3) величиной (модулем). Сила – причина ускорения, т.е. изменения скорости тела.

Силу можно найти по второму закону Ньютона:

Равнодействующая всех сил, приложенных к телу, равна произведению массы тела на его ускорение: = m . ( = ₁ + ₂ + ₃ + …+ )

В международной системе единиц силу измеряют в ньютонах (Н).

Из закона следует: чем больше сила, тем больше ускорение тела. Разные тела под действием одной и той же силы приобретают разные ускорения. Свойство тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью. Свойство инертности, присущее всем телам, состоит в том, что для изменения скорости тела требуется некоторое время. Количественной мерой инертности тела является его масса (m). Массу в международной системе единиц измеряют в килограммах (кг). Чем большей массой обладает тело, тем меньшее ускорение оно получает при взаимодействии.

Третий закон Ньютона объясняет, как вообще возникает сила.

Третий закон Ньютона:

Из закона следует: 1)силы появляются парами; 2)эти силы одной и той же природы; 3) эти силы приложены к разным телам – они не уравновешиваются. Уравновешиваться могут силы, приложенные к одному и тому же телу. Законы Ньютона выполняются в ИСО.

Билет 3.

Импульс тела. Закон сохранения импульса. Реактивное движение в природе и технике.

Второй закон Ньютона = m можно записать по-другому, если учесть, что = Тогда = m , где t – время действия силы , за которое произошло изменение скорости от до . По-другому эту формулу можно записать:

= m . Это другая форма записи второго закона Ньютона.

Импульсом тела называется векторная величина, равная произведению массы тела m на его скорость : = m Импульс – это векторная величина. Импульс направлен также как и скорость. В СИ импульс измеряют в (килограмм на метр в секунду). Импульс обладает важным свойством – это свойство сохранения. В чём оно состоит? Свойство сохраняться – это свойство оставаться неизменным. Оно справедливо для замкнутой системы тел. Система тел, взаимодействующих только друг с другом и не взаимодействующих ни с какими другими телами, называется замкнутой. Закон сохранения импульса: векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется.

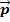
Для двух взаимодействующих тел закон сохранения импульса имеет вид:

+ = + ,где —массы тел; — скорости тел до взаимодействия; , — скорости тел после взаимодействия.

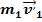
Билет 4.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник