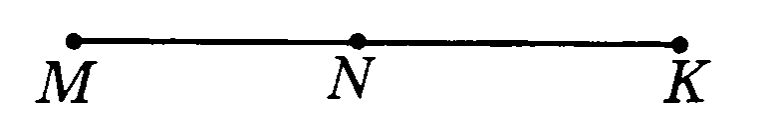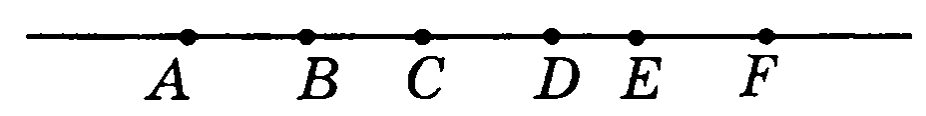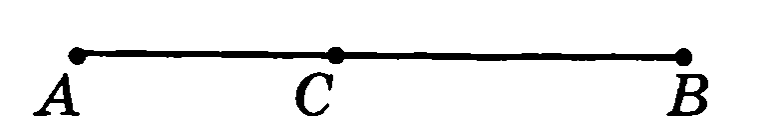на рис 5 точка y удовлетворяет условиям
Проверочная работа «Сравнение и измерение отрезков», 7 класс
Проверочная работа проводилась после изучения темы «Сравнение и измерение отрезков» (УМК Атанасян). Работа на 2 варианта с ответами. Составлена на основе сборника заданий для тематического и итогового контроля знаний по геометрии в 7 классе (автор А.П. Ершова)
Просмотр содержимого документа
«Проверочная работа «Сравнение и измерение отрезков», 7 класс»
«Сравнение и измерение отрезков»
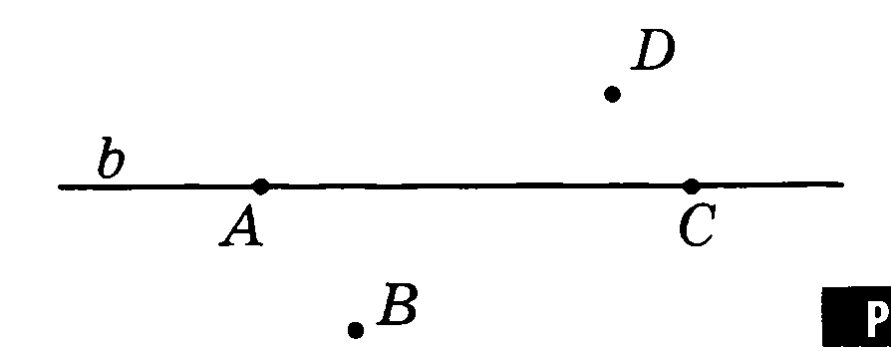
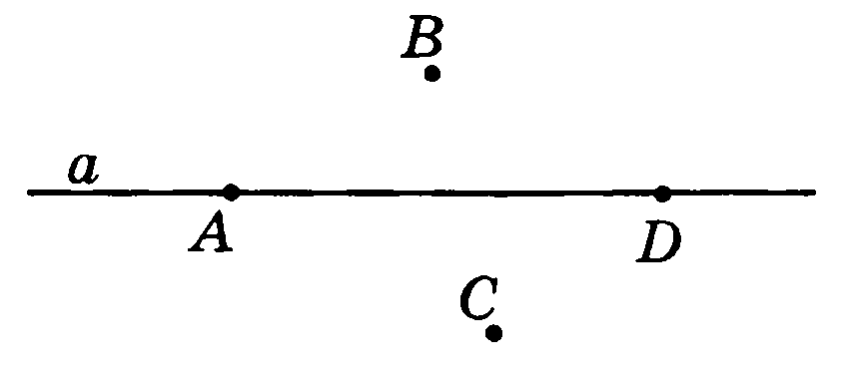
Какие из точек А, В, С, D лежат на прямой b, а какие не лежат?
Назовите все отрезки, изображенные на рисунке
На рисунке MN = 8,7 см, КМ = 19,2 см. Найдите NК
На рисунке LM = 15 см, NK = 16 см, MK = 24 см. Найдите MN, LK, NL.
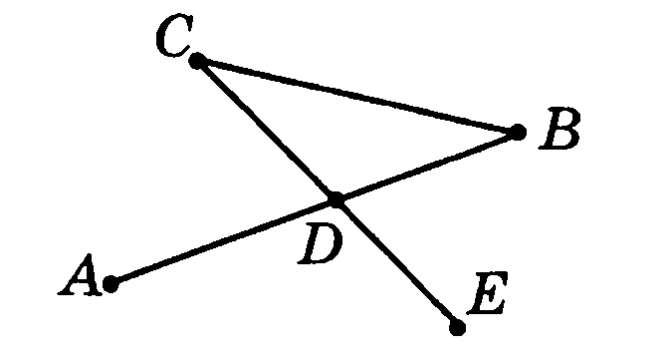
На рисунке точке Y удовлетворяет условиям:
принадлежит отрезку AD
не принадлежит отрезку CF
точка А не принадлежит лучу YC
Точка Y совпадает с одной из данных точек. С какой?
«Сравнение и измерение отрезков»
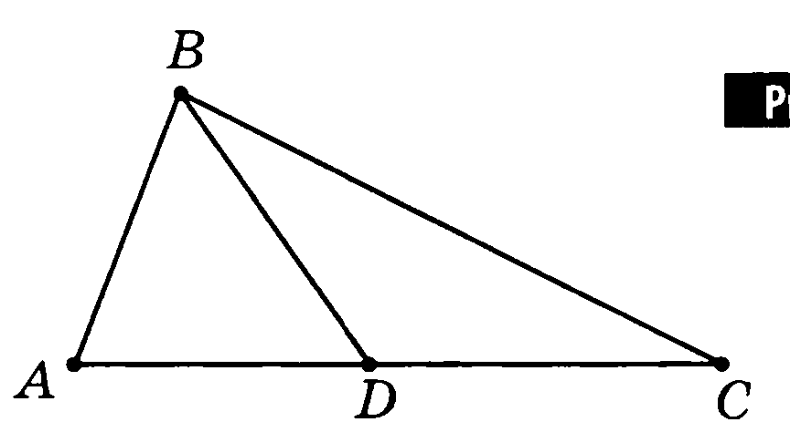
Какие из точек А, В, С, D лежат на прямой а, а какие не лежат?
Назовите все отрезки, изображенные на рисунке
На рисунке АВ = 18,4 см, СВ = 10,8 см. Найдите АС.
На рисунке АС = 9 см, СВ = 4 см, ВD = 12 см. Найдите АВ, СD, АD.
На рисунке точке Х удовлетворяет условиям:
принадлежит отрезку ВF
не принадлежит отрезку АD
точка А не принадлежит лучу CХ
Точка Х совпадает с одной из данных точек. С какой?
Множество точек. Изображение некоторых множеств точек на плоскости.
В первом случае прямые параллельны оси ординат, во втором – абсцисс.
На координатной прямой неравенству х 3. Проанализируем, что это за точки:
— множество точек, абсцисса которых больше или равна 3
— точки, лежащие правее прямой х = 3 и на прямой.
Алгоритм построения будет иметь вид:
— строим в координатной плоскости прямую: х = 3;
— определяем, где будут находиться точки, абсцисса которых больше 3; ответ – правее;
— множество всех точек удовлетворяющих условию х > 3 покажем при помощи штриховки;
х > 3 задает полуплоскость, находящаяся правее прямой х = 3 и все точки этой прямой. Прямую изображаем одной цельной линией, этим указываем, что все точки расположенные на прямой так же включены во множество.
Представим множество точек, удовлетворяющих условию у 1.
Следовательно, они будут находиться выше прямой у = 1. В соответствии со знаком неравенства точки прямой у = 1 не удовлетворяют условию y > 1. Графически мы это покажем, изобразив прямую у = 1 пунктиром.
Представим множество точек, соответствующих условию у > 1 так:
На рис 5 точка y удовлетворяет условиям
Найдите все целочисленные значения параметра а, при каждом из которых система
имеет единственное решение.
Следовательно, данная система имеет единственное решение тогда и только тогда, когда второе уравнение системы имеет единственное решение на отрезке 1 ≤ x ≤ 5.
Рассмотрим квадратичную функцию
Её график — парабола, направленная ветвями вверх. Поскольку свободный при любом a, то корни этой функции имеют разные знаки. Известно, что в этом случае единственный положительный корень функции
лежит на отрезке 1 ≤ x ≤ 5 тогда и только тогда, когда
и
Получаем систему
Поскольку любое решение полученного неравенства должно удовлетворять условию то есть
и по условию a — целое число, то решениями неравенства могут быть только
Из этих условий проверкой получаем все решения: −2, ±1, 0.
Ваше рассуждение было бы верным, если бы во втором уравнении системы присутствовала переменная .
Найдите все целочисленные значения параметра а, при каждом из которых система
имеет единственное решение.
Следовательно, данная система имеет единственное решение тогда и только тогда, когда второе уравнение системы имеет единственное решение на отрезке 2 ≤ x ≤ 5.
Рассмотрим квадратичную функцию
Её график — парабола, направленная ветвями вверх. Поскольку свободный член при любом a, то корни этой функции имеют разные знаки. Известно, что в этом случае единственный положительный корень функции
лежит на отрезке 2 ≤ x ≤ 5 тогда и только тогда, когда
и
Получаем систему
Поскольку любое решение полученного неравенства должно удовлетворять условию то есть
и по условию a — целое число, то решениями неравенства могут быть только
Из этих условий проверкой получаем все решения: −2, ±1, 0.
Аналоги к заданию № 512340: 512382 Все
Извините, не совсем понятно почему функция от 2 меньше либо равно 0,а функция от 5 больше либо равно 0.Объясните,пожалуйста.Спасибо.
Андрей, попробуйте нарисовать параболу с описанными свойствами: ветви вверх, с отрицательным свободным членом, положительный корень лежит между числами 2 и 5. И вы сами увидите ответ на свой вопрос
При каждом а решите систему уравнений
Запишем второе уравнение в виде
Геометрический смысл уравнения состоит в том, что сумма расстояний от точек до точек
и
равно
Поскольку расстояние между точками
и
тоже равно
это означает, что точка
должна лежать на отрезке, соединяющем точки
и
Другими словами, она удовлетворяет уравнению
и условию
Таким образом, исходная система равносильна системе
Подставив 2а в первое уравнение, получаем
Поскольку функция возрастающая (как сумма двух возрастающих), каждое значение она принимает ровно один раз. Поэтому решение
— единственное, ему соответствует
Ответ: если то
при остальных а нет решений.
А как нашли, что х=5/2?
угадали корень уравнения:
Найдите все неотрицательные значения a, при каждом из которых система уравнений
имеет единственное решение.
Первому уравнению системы удовлетворяют те и только те точки которые лежат на отрезке AB прямой, соединяющей точки
и
поскольку уравнение задаёт множество точек
сумма расстояний от каждой из которых до точек А и В равна
что равно длине отрезка АВ.
Второму уравнению системы удовлетворяют те и только те точки которые лежат на прямой
параллельной оси абсцисс и проходящей через точку
По условию Если
то точки В и О совпадают, и система не имеет решений. Для
условие задачи выполнено тогда и только тогда, когда точка С лежит между точками О и В, причём если точка С совпадает с точкой O или с точкой В, то условие задачи выполнено.
Решим неравенство Имеем:
Ответ:
Задача станет интереснее, если отказаться от условия неотрицательности параметра. При a Ответ:
Отсутствует случай a
Найдите все значения параметра при каждом из которых система
имеет единственное решение.
Уравнение означает, что сумма расстояний от точки
до точек
и
равна
но эта сумма расстояний всегда больше, чем
если только точка
не лежит на отрезке с концами
и
Значит, множество решений при
— это отрезок с концами
и
При
множество решений — это
Множество решений неравенства — круг на плоскости с координатами
с центром в начале координат и радиусом
Отсюда получаем необходимое условие существование единственного решения — отрезок с концами
и
должен пересекаться с данным кругом в единственной точке. Это возможно при
(когда отрезок превращается в точку), а также когда отрезок касается границы круга. Из симметрии точка касания лежит в середине этого отрезка. Расстояние от середины отрезка до начала координат равно
В случае касания это расстояние должно совпадать с радиусом круга, откуда получаем уравнение
Таким образом, система имеет единственное решение при
и
Ответ:
На рис 5 точка y удовлетворяет условиям
На рисунке изображен график производной функции определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите сумму целых точек, входящих в эти промежутки.
Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых ее производная неотрицательна, то есть промежуткам (−6; −5,2] и [2; 6). Данные промежутки содержат целые точки 2, 3, 4 и 5. Их сумма равна 14.
Здравствуйте! Как я понимаю, в точке х=2 производная равна нулю, следовательно, это точка минимума, то есть число 2 не включается в интервал, и тогда сумма равна 3+4+5=12
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке [a;b]. Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке [2; 6) функция возрастает.
После нахождения промежутков просят найти какие целые числа попадают в эти промежутки.
В условии и в решении не идёт речи о возрастании в точке.
Речь в задании о промежутках возрастания.
Господа, добрый день!
На мой взгляд, в решении ошибка: x=2 не должен включаться в решение. В учебнике Ильина, Позняка «Основы математического анализа» (гл. 8 Основные теоремы о непрерывных функциях, § 7 Возрастание (убывание) функции в точке (стр 260 в 7-м издании 2005 года) дано такое определение:
Говорят, что функции f(x) возрастает (убывает) в точке c, если найдется такая окрестность точки c, в пределах которой f(x)>f(c) при x>c и f(x) c и f(x)>f(c) при x
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех интервалах, на которых функция возрастает, т. е. на интервалах (−3; 0) и (4,2; 7). В них содержатся целые точки −2, −1, 5 и 6, всего их 4.