как доказать что прямые в пространстве пересекаются
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №5. Взаимное расположение прямых в пространстве
Перечень вопросов, рассматриваемых в теме
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Два отрезка называются параллельными, если они лежат на паралельных прямых.
Открытый электронный ресурс:
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)
Рисунок 1 – скрещивающиеся прямые
На прошлом уроке в качестве наглядного примера нами был приведен куб.
Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.
Примеры скрещивающихся прямых вокруг нас:
Одна дорога проходит по эстакаде, а другая под эстакадой
Горизонтальные линии крыши и вертикальные линии стен
Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).
Рисунок 2 – скрещивающиеся прямые АВ и СD
Итак, возможны три случая расположения прямых в пространстве:
Разберем и докажем еще одну теорему о скрещивающихся прямых.
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Рисунок 3 – прямые АВ, СD, DЕ
Любая прямая, например ОО1, рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О1А1 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)
Рисунок 4 – сонаправленные лучи
Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)
Доказательство:
при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.
Отметим на сторонах угла O произвольные точки A и B.
На соответствующих сторонах угла O1 отложим отрезки OA1 и O₁B₁ равные соответственно ОA и OB.
2. В плоскости рассмотрим четырехугольник OAA1O1.
Так как противолежащие стороны OA и O1A1 этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA1 и OO1.
3. В плоскости, аналогично можно доказать, что OBB1O1 параллелограмм, поэтому равны и параллельны стороны ВВ1 и OO1.
4. Если две отрезка AA1 и BB1 равны параллельны третьему отрезку OO1, значит, они равны и параллельны, т. е. АА1||BB1 и AA1 = BB1.
По определению четырехугольник АВВ1А1 – параллелограмм и из этого получаем АВ=А1В1.
5.Из выше построенного и доказанного АВ=А1В1, ОA =O1A1 и OB =O1B1 следует, что треугольники AOB и A1 O1 B1. равны по трем сторонам, и поэтому О= О1.
Рисунок 5 – равные углы с сонаправленными сторонами
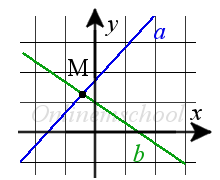
Пересечение прямых. Точка пересечения двух прямых
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
Вычтем из первого уравнения второе
Из первого уравнения найдем значение x
Подставим значение x во второе уравнение и найдем значение y
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
В первое уравнение подставим значения x и y из второго и третьего уравнений.
Подставим значение t во второе и третье уравнение
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
Из второго уравнения выразим y через x
Подставим y в первое уравнение
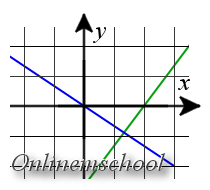
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
Вычтем из первого уравнения второе
Ответ. Прямые не пересекаются (прямые параллельны).
Решение: Подставим координаты точки N в уравнения прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
Решение: Составим систему уравнений
К шестому уравнению добавим пятое уравнение
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
Подставим значение t из шестого уравнения в остальные уравнения
Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Точка пересечения прямых в пространстве − теория, примеры и решения
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
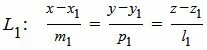 , , | (1) |
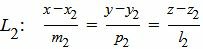 , , | (2) |
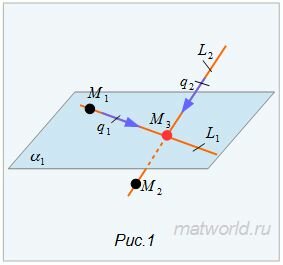
Найти точку пересечения прямых L1 и L2 (Рис.1).
 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (7) и (8):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
Так как левые части уравнений (14) равны, то можем записать:
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
Представим уравнение (20) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (22) и (23):
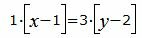 |
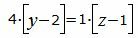 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
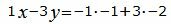 |
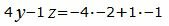 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (7) и (8)
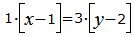 |
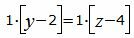 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
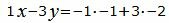 |
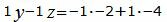 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
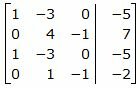 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
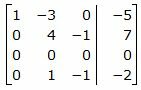 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
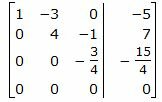 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
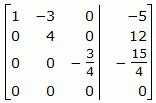 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
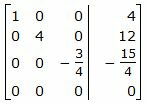 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
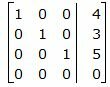 |
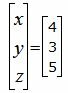 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
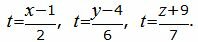 |
Из равентсв выше получим каноническое уравнение прямой:
Представим уравнение (33) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
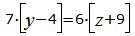 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
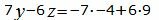 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (38) и (39)
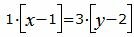 |
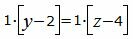 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
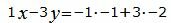 |
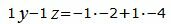 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
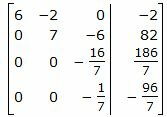 |
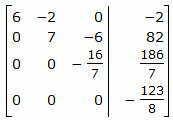 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №5. Взаимное расположение прямых в пространстве
Перечень вопросов, рассматриваемых в теме
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Два отрезка называются параллельными, если они лежат на паралельных прямых.
Открытый электронный ресурс:
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)
Рисунок 1 – скрещивающиеся прямые
На прошлом уроке в качестве наглядного примера нами был приведен куб.
Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.
Примеры скрещивающихся прямых вокруг нас:
Одна дорога проходит по эстакаде, а другая под эстакадой
Горизонтальные линии крыши и вертикальные линии стен
Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).
Рисунок 2 – скрещивающиеся прямые АВ и СD
Итак, возможны три случая расположения прямых в пространстве:
Разберем и докажем еще одну теорему о скрещивающихся прямых.
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Рисунок 3 – прямые АВ, СD, DЕ
Любая прямая, например ОО1, рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О1А1 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)
Рисунок 4 – сонаправленные лучи
Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)
Доказательство:
при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.
Отметим на сторонах угла O произвольные точки A и B.
На соответствующих сторонах угла O1 отложим отрезки OA1 и O₁B₁ равные соответственно ОA и OB.
2. В плоскости рассмотрим четырехугольник OAA1O1.
Так как противолежащие стороны OA и O1A1 этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA1 и OO1.
3. В плоскости, аналогично можно доказать, что OBB1O1 параллелограмм, поэтому равны и параллельны стороны ВВ1 и OO1.
4. Если две отрезка AA1 и BB1 равны параллельны третьему отрезку OO1, значит, они равны и параллельны, т. е. АА1||BB1 и AA1 = BB1.
По определению четырехугольник АВВ1А1 – параллелограмм и из этого получаем АВ=А1В1.
5.Из выше построенного и доказанного АВ=А1В1, ОA =O1A1 и OB =O1B1 следует, что треугольники AOB и A1 O1 B1. равны по трем сторонам, и поэтому О= О1.
Рисунок 5 – равные углы с сонаправленными сторонами