как доказать что отрезки равны
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
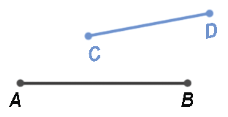
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
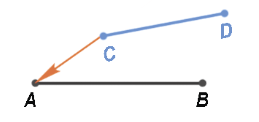
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
Так как отрезки AB и AC имеют одинаковую длину, то
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
Сравнение отрезков. Действия над отрезками.
Равные и неравные отрезки
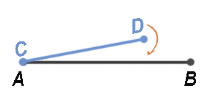
Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.
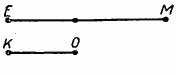
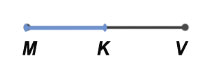
Сравним два отрезка КО и ЕМ (рис.).
Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.
Записывается это тaк: ЕМ > КО, КО 1 /5 часть отрезка МN.
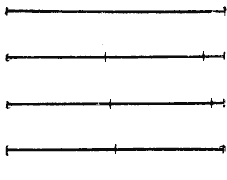
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).
Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла
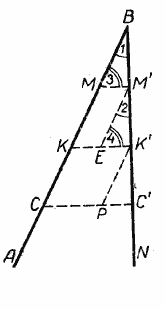
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.
На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.
Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.
Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:
∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;
∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).
ВМ = МК по построению;
МК = М’Е, как противоположные стороны параллелограмма.
Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.
Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.
Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.
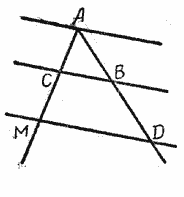
В этом случае вершину угла на чертеже можно не отмечать (рис.).
Теорема справедлива и для случая, когда прямые КО и МР параллельны.
Пропорциональные отрезки
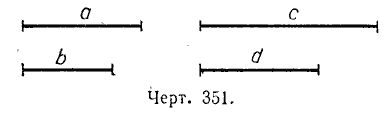
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /4 = 20 /5; 2 /3 = 4 /6 To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.
отрезки а, b, c, d называются пропорциональными.
В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.
Поскольку в пропорции a /b = c /d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /x = c /d x = a • d /c
Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.
а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.
Чтобы убедиться в этом, переставим средние члены в этой пропорции.
А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.
В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.
Построение пропорциональных отрезков
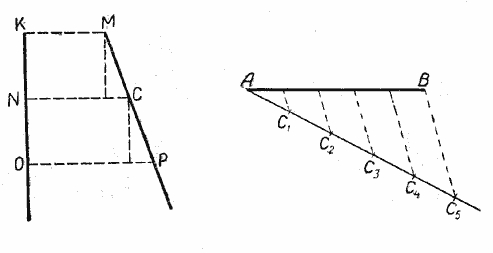
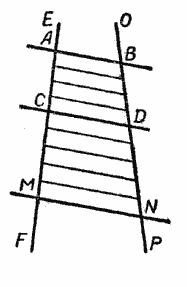
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).
Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.
Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.
Например, р = 4 см. и q = 5 см.
Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.
Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.
Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /AM = BD /BN,
Теорема будет справедлива и при любых других целых значениях р и q.
Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.
Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.
Приемы учебной работы при обучении решению задач на доказательство
Разделы: Математика
Обучение доказательствам – одна из важнейших целей обучения математике.
Именно при выполнении доказательств оттачивается логическое мышление учеников, разрабатываются логические схемы решения задач, возникает потребность учащихся в обосновании математических фактов.
Начиная изучать геометрию, учащиеся способны осознать необходимость доказательства, однако осуществлению доказательства им только предстоит научиться.
С задачами на доказательство учащиеся встречаются при изучении второй темы курса геометрии 7-го класса “Треугольники”. Опыт проведения доказательств отсутствует. Учащиеся не владеют геометрическим языком, многие не понимают смысла слова “доказать”, поэтому испытывают большие трудности. Я решаю эту проблему, предоставляя учащимся образцы (алгоритмы) доказательства. В ходе изучения теоретического материала вместе с учениками составляем алгоритмы решения задач каждого вида и красочно оформляем их в виде книжки.
Эта книга помогает учащимся в затруднительных случаях быстро найти сходную задачу, вспомнить алгоритм решения, составить план решения.
Обучение решению задач веду постепенно.
7-й класс
Тема “Параллельные прямые”
1.Алгоритм решение задачи: доказать, что прямая … параллельна прямой ….
Тема “Прямоугольный треугольник”
1.Алгоритм решение задачи: доказать, что прямоугольные треугольники … равны
8-й класс
Тема “Параллелограмм”.
1.Алгоритм решение задачи: доказать, что четырехугольник…. будет параллелограммом.
Тема “Подобие треугольников”.
1.Алгоритм решение задачи: доказать, что треугольник …. подобен треугольнику…
Принцип пошаговости формирует навыки решения задач и навыки построения логических цепочек доказательства.
Решение задач учу начинать с предложения “Чтобы доказать, что …”. Ученик называет то, что требуется доказать в конкретной задаче и ведет доказательство по соответствующему алгоритму. Такой ход решения позволяет учащимся понимать смысл поставленной задачи, выстраивать аргументацию, формирует умение анализировать, развивает логическое мышление.
Работая в дальнейшем по модели, ученик на каждом шагу контролирует свои действия, обращаясь к выведенному алгоритму. На любом этапе работы ученик может по сигналу учителя передать “эстафету” решения любому ученику. Этим достигается предельное внимание при решении задачи.
Красочно оформленные алгоритмы учащиеся запоминают быстро. И к концу изучения темы “Признаки равенства треугольников” многие учащиеся хорошо проводят доказательные рассуждения, точно и грамотно выражают свои мысли. Данные алгоритмы учащиеся применяют и при доказательстве теорем.
Разработанные алгоритмы позволили логически упорядочить материал, дать его компактное и наглядное изложение. Они способствуют как подсознательному запоминанию, так и осознанному усвоению материала. При пользовании алгоритмами учащиеся лучше осмысливают, осознают логические взаимосвязи. Это помогает им научиться решать задачи.
Пример решения задачи учениками 7-го класса по теме
“Признаки равенства треугольников”
Доказать BD – биссектриса 
(Устно). Чтобы доказать, что BD биссектриса, нужно доказать, что угол ABD равен углу DBC.Чтобы доказать, что два угла равны, нужно доказать, что равны треугольники, содержащие эти углы
Работа в тетради. Рассмотрим 

(Устно) Чтобы доказать, что два треугольника равны, найдем у них три равных элемента.
АВ = ВС по условию задачи,
АD = DC по условию задачи,
Значит 

В равных треугольниках соответственные элементы равны.
Значит, угол ABD равен углу DBC.
Следовательно, BD-биссектриса по определению биссектрисы угла.
Алгоритмы решения задач на доказательство.
Задача на доказательство – это утверждение, которое необходимо доказать с помощью аксиом и теорем.
Доказательство ведется на основе признаков равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Алгоритм решения задачи: доказать, что отрезок … равен отрезку ….
В равных треугольниках соответственные элементы равны.
Сравнение отрезков
Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:
Метод наложения:
Пусть нам даны два отрезка AB и СD:
Совместим начало отрезка AB и СD (точки A и С).
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.
Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.
Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.
Рассмотрим еще одну пару отрезков HG и ST.
Совместим начало отрезка HG и ST.
Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.
В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.
Вывод:
Измерение длин:
Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.
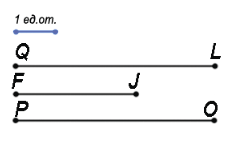
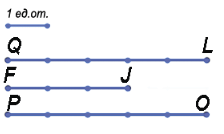
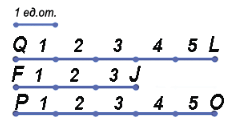
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.
Наложим единичный отрезок на данные.
Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.
Поделись с друзьями в социальных сетях:
Что такое аксиома, теорема и доказательство теоремы
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Записывайся на онлайн обучение по математике для учеников с 1 по 11 классы!
Доказательство через синтез
Рассмотрим пример синтетического способа доказательства.
Теорема: сумма углов треугольника равна двум прямым.
Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.
Доказательство:
Проведем прямую DE, так чтобы она была параллельна AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.
Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Доказательство через анализ
Рассмотрим пример аналитического способа доказательства.
Теорема: диагонали параллелограмма пересекаются пополам.
Дан параллелограмм: ABCD.
Доказательство:
Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.
Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол напротив стороны а.
Следствия из теоремы косинусов:
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.