как доказать что четырехугольник можно вписать в окружность
Четырехугольники, вписанные в окружность. Теорема Птолемея
Вписанные четырёхугольники и их свойства
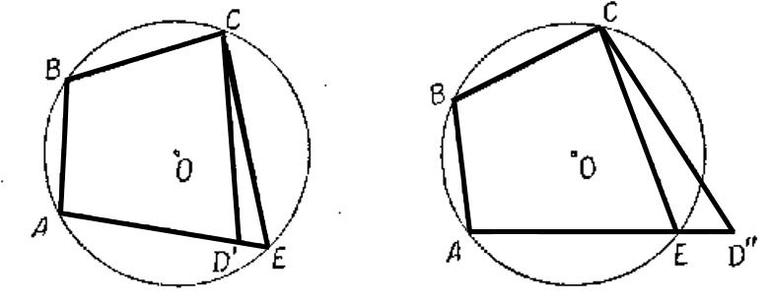
Теорема 1 доказана.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | ||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||||||||||||||||||||||||
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | |||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | ||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |
| Окружность, описанная около ромба | ||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | ||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | ||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | ||
 | ||
| Окружность, описанная около ромба | ||
 Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||
| Окружность, описанная около трапеции | ||
 Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||
| Окружность, описанная около дельтоида | ||
 Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||
| Произвольный вписанный четырёхугольник | ||
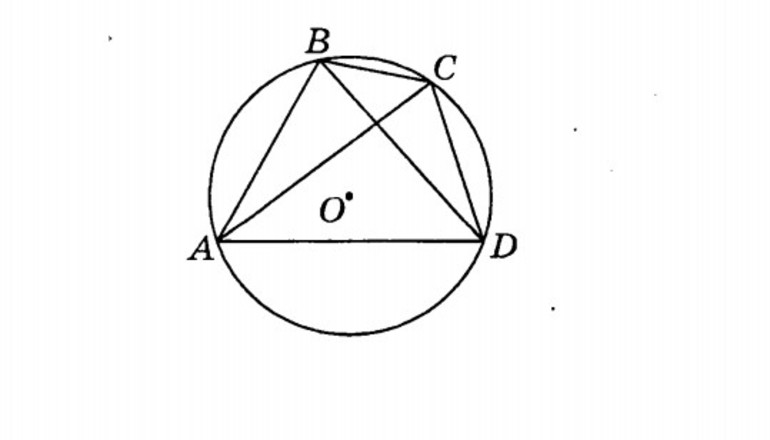
 Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, Теорема ПтолемеяДокажем, что справедливо равенство: Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4). откуда вытекает равенство:
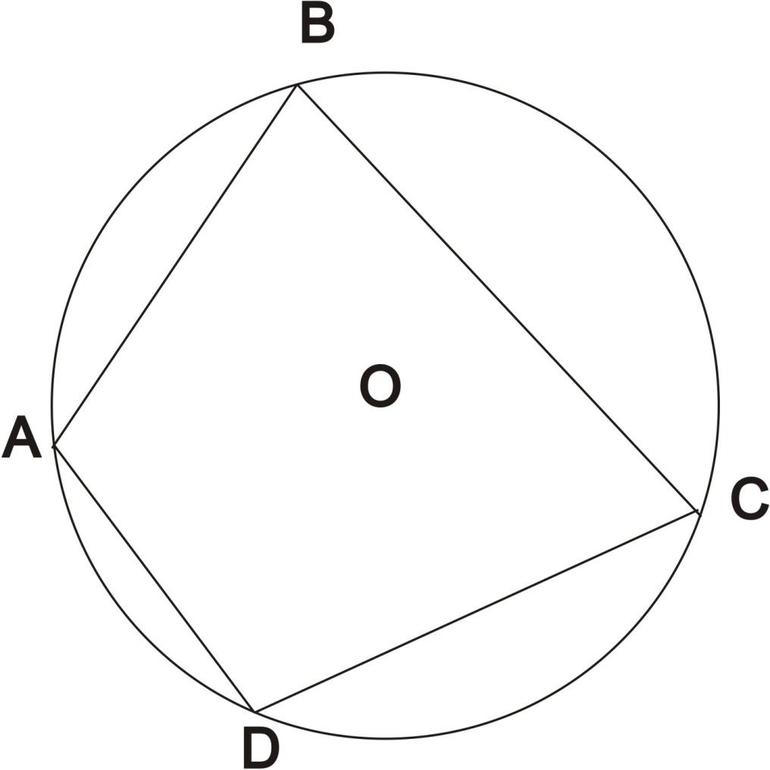
Вписанный четырехугольник и его свойства (ЕГЭ 2022)Мы видели, что вокруг всякого треугольника можно описать окружность. Вот так: Вопрос: а можно ли получить вписанный четырехугольник? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника? Сейчас мы это выясним! Вписанный четырехугольник — коротко о главном
\( \displaystyle \angle B+\angle D=180<>^\circ \).
Вписанный четырехугольник — определения и теоремыВот оказывается, что это неправда! НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:
На нашем рисунке: \( \displaystyle \alpha +\beta =180<>^\circ \) Посмотри, углы \( \displaystyle \alpha \) и \( \displaystyle \beta \) лежат друг напротив друга, значит, они противоположные. А что же тогда с углами \( \displaystyle \varphi \) и \( \displaystyle \psi \)? Они вроде бы тоже противоположные? Можно ли вместо углов \( \displaystyle \alpha \) и \( \displaystyle \beta \) взять углы \( \displaystyle \varphi \) и \( \displaystyle \psi \)? Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет \( \displaystyle 180<>^\circ \). Оставшиеся два угла тогда сами собой тоже дадут в сумме \( \displaystyle 180<>^\circ \). Не веришь? Давай убедимся. Пусть \( \displaystyle \alpha +\beta =180<>^\circ \). Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, \( \displaystyle 360<>^\circ \). То есть \( \displaystyle \alpha +\beta +\varphi +\psi =360<>^\circ \) — всегда! \( \displaystyle 180<>^\circ \) Так что запомни крепко-накрепко:
Доказательство смотри чуть дальше. А пока давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна \( \displaystyle 180<>^\circ \). Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма? Вписанный параллелограммПопробуем сперва «методом научного тыка»: Вот как-то не получается. Теперь применим знание: Предположим, что нам как-то удалось посадить на параллелограмм \( \displaystyle ABCD\) окружность. Тогда непременно должно быть: \( \displaystyle \alpha +\beta =180<>^\circ \), то есть \( \displaystyle \angle B+\angle D=180<>^\circ \). А теперь вспомним о свойствах параллелограмма: у всякого параллелограмма противоположные углы равны. То есть \( \displaystyle \angle B = \angle D\). У нас получилось, что \( \displaystyle \left\< \begin А что же углы \( \displaystyle A\) и \( \displaystyle C\)? Ну, то же самое конечно. \( \displaystyle ABCD\) – вписанный → \( \displaystyle \angle A+\angle C=180<>^\circ \) → \( \displaystyle \angle A=90<>^\circ \) \( \displaystyle ABCD\) — параллелограмм→ \( \displaystyle \angle A=\angle C\) → \( \displaystyle \angle C=90<>^\circ \) Четырехугольник, вписанный в окружностьРассмотрим, что такое четырехугольник, вписанный в окружность и около какого четырехугольника можно описать окружность. Четырехугольник называется вписанным в окружность, если все вершины четырехугольника лежат на окружности. Четырехугольник ABCD — вписанный в окружность. Все его вершины — точки A, B, C, D — лежат на окружности. 1) Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º. 2) Если сумма противолежащих углов четырехугольника равна 180º, то этот четырехугольник можно вписать в окружность. вписанный в окружность. 1) Из всех параллелограммов вписать в окружность можно только прямоугольник (в том числе, в квадрат).
Радиус описанной около прямоугольника окружности равен половине его диагонали. Через стороны прямоугольника радиус описанной окружности равен Если стороны прямоугольника обозначить как a и b, то 2) Из всех трапеций вписать в окружность можно только равнобедренную трапецию.
Общие сведенияФигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него. Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом. Основные правилаВыпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия: Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом. Свойства и утвержденияПри решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
Формулы и соотношенияОчень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами. Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника. Периметр и полупериметрПериметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д. Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой. Понятие площадиКогда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты. Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2. Диагонали и углыДля вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d. При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2). Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD). Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом: В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½). В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры: В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения: Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается. Параметры для окружностиРадиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
| ||











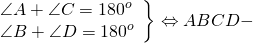
 Центр описанной около прямоугольника окружности — точка пересечения его диагоналей.
Центр описанной около прямоугольника окружности — точка пересечения его диагоналей.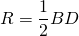
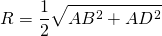
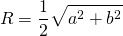
 Радиус описанной около трапеции окружности можно найти как радиус окружности, описанной около одного из треугольников — вершин трапеции:
Радиус описанной около трапеции окружности можно найти как радиус окружности, описанной около одного из треугольников — вершин трапеции: