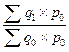Статистика что такое индекс

Понятие и классификацию индексов в статистике

Индекс (лат. index — показатель, указатель, опись, ре­естр) представляет собой относительный показатель, вы­ражающий соотношение значений признака изучаемого явления во времени, в пространстве или сравнение фак­тических данных с данными, принятыми за основу для сравнения.

• для характеристики выполнения плана (например, плана по выпуску продукции (работ, услуг), снижению себестоимости продукции (работ, услуг), росту производительности труда),

• для изучения динамики (например, исследование изменения оптовых и розничных цен на отдельные виды товаров, объёма произведенной продукции (работ, услуг), реальных и номинальных доходов населения),

• для сравнения уровней социально-экономических явлений по территориям.

Задачи, решаемые с помощью экономических индек­сов:

§ расчет динамики среднего экономического показателя;

§ расчет соотношения показателей по регионам;

§ расчет влияния изменений значений одних показате­лей на динамику других показателей;

§ пересчет значения показателей из фактических цен в сопоставимые.

Индексы относят к важнейшим обобщающим показа­телям.

Классификация экономических индексов представлена на рисугке 7.1.

При расчете индексов сравниваются значения показа­теля в отчетный период со значением этого же показателя за предыдущий (базисный) период. В качестве базы сравнения также могут использоваться прогнозные и плановые показа­тели. Динамические индексы бывают базисными и цепными;

Цепные индексы получают сопоставлением индексируемой величины последующего периода с показателем предшествующего ему периода. В этом случае база сравнения непрерывно меняется.

Базисные индексы получают сопоставлением индексируемого показателя каждого периода с соответствующим показателем какого-то одного определенного периода, принятого за базу сравнения.

Правила построения индексов:

• признак, характеризующий отчетный период, относится к признаку, характеризующему базисный период. Но существуют исключения — показатели, имеющие между собой обратно пропорциональную зависимость;

• при изучаемом первичном признаке берется влияющий на него признак-вес на неизменном базисном уровне. При изучении вторичного признака используется влияющий на него признак-вес на неизменном уровне отчетного года.

Индивидуальный индекс — это относительный показатель, выражающий изменение отдельного элемента сложного экономического явления. Индивидуальный индекс обозначается буквой “i”.

где i_x — рассчитываемый индивидуальный индекс по фактору х;

Х₁— величина отчетного показателя; Х₀ — величина базисного показателя;

если за базу сравнения принимается нормативный (х_н), плановый (х_пл), эталонный (х_э) показатель, то

i_x = x₁/x_пл, где х_пл — плановый показатель;

i_x = x₁/x_э где х_э — эталонный показатель.

КЛАССИФИКАЦИЯ ЭКОНОМИЧЕСКИХ ИНДЕКСОВ

Рисунок 7.1. Классификация индексов.

Сводный индекс выражает соотношение величин сложного экономического явления, состоящего из элементов непосредственно несоизмеримых. Сводный индекс обозначается буквой “I”

Основной формулой для расчета сводного индекса является агрегатная формула, в которой с помощью весов индекса несоизмеримые величины приводятся к соизмеримому виду. Например, индекс физического объёма продукции можно рассчитать по следующей формуле:

I_q =

Агрегатный индекс является формой сводного индекса, используемой для характеристики изменения сложного экономического явления.

Элементы агрегатной формы,:

· индексируемая величина, изменение которой показывает индекс (х);

· некоторая постоянная величина, называемая весом индекса (f); с помощью весов несоизмеримые величины сложного социально-экономического явления приводят к сопоставимому виду.

Сводные индексы
Групповой индекс	Общий индекс
рассчитывается для группы элементов, входящих в общую совокупность.	рассчитывается для всей совокупности элементов изучаемого явления.

Средние индексы — это средняя величина из индивидуальных индексов. В статистике рассчитываются взвешенные средние арифметические и средние гармонические индексы. Термином “средний индекс” иногда называют сводный индекс, так как он характеризует в среднем изменение элементов, составляющих сложное экономическое явление. Средний индекс всегда тождественен агрегатному индексу.

Правила построения средних индексов:

§ для индекса количественного показателя используют формулу среднего арифметического индекса,

Средний арифметический индекс тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса, рассчитанного по формуле средней арифметической, будет равна агрегатному индексу.

Средний арифметический индекс физического объема продукции вычисляется по формуле:

.

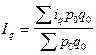
Средний арифметический индекс производительности труда определяется следующим образом:

.

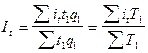
В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он носит название индекса Струмилина и определяется следующим образом:

.

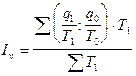
Индекс показывает, во сколько раз возросла (уменьшилась) производительность труда, или сколько процентов составил рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности.

Индексы других качественных показателей (цен, себестоимости и т.д.) определяется по формуле средней гармонической взвешенной величины.

Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Средние индексы широко используются при расчете агрегатных индексов. Наиболее известными являются индексы Доу-Джонса, Стэндарда и Пура.

Индекс Доу-Джонса (Dow Jones Industrial Average Index) определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, и ежедневно публикуется их значение на момент закрытия биржи. Групповые индексы определяются по ценам акций 30 промышленных, 20 транспортных и 15 компаний сферы услуг. Общий индекс рассчитывается по всем 65 компаниям. Их перечень был составлен в 1928г. в качестве базисного выбран 1920г. первоначальная методика исчисления индекса была разработана основателем и редактором крупнейшей в США газеты «Уолл-Стрит джорнел» Чарльзом Доу.

Источник

Тема 7.1. Понятие индексов в статистике.

1. Понятие индекса, сущность индексного метода.

2. Индивидуальные и сводные индексы.

3. Индексы количественных и качественных показателей.

4. Индексы переменного, фиксированного состава.

1. Понятие индекса, сущность индексного метода

Слово «индекс» означает «показатель». Как правило, этот показатель используется для обобщающей характеристики изменений (например, индекс инфляции, индекс Доу-Джонса). Иногда термин «индекс» используют как обобщающий показатель состояния (например, индекс интеллектуального развития IQ). Мы будем рассматривать индексы как показатели изменений.

Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня этого же явления в других условиях. Различие условий может проявляться:

— во времени (индексы динамики);

— в пространстве (территориальные индексы);

— в выборе базы сравнения (план, договор, норматив).

На практике индексный метод применяют для соизмерения сложных явлений (т.е. таких, количественное выражение которых предполагает значительные подсчеты), для выявления роли отдельных факторов в формировании какой-либо величины (например, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров и тарифов и за счет соотношения в объеме перевозок разных видов транспорта), для сравнения уровня явления не только с прошлым периодом, но и с другой территорией или нормативом.

Все экономические индексы можно классифицировать по следующим признакам:

— степень охвата явления (индивидуальные и общие);

— база сравнения (динамики, территориальные, выполнения плана);

— вид весов (с постоянными или переменными весами);;

— форма построения (агрегатные и средние);

— характер объекта исследования (и. цен, физического объема, структурных сдвигов);

— состав явления (и. количественных и качественных показателей);

— период исчисления. (годовые, квартальные, …).

По степени охвата явления индексы бывают индивидуальные и сводные. По базе сравнения – динамические, территориальные, нормативные. По виду весов – с постоянными и переменными весами. В зависимости от формы построения различают агрегатные и средние. По характеру объекта исследования – индексы количественных и качественных показателей. По составу— индексы количественных и качественных показателей. По периоду исчисления – годовые, квартальные и т.д.

Каждый индекс включает два вида данных: оцениваемые, текущие (их обозначают «1») и данные, с которыми сравнивают, база сравнения (их обозначают «0»).

р “price” – цена, зарплата (любой стоимостной эквивалент),

Условие применения индексного метода – наличие жестко детерминированной связи между признаками. Связь между признаками может быть:

— Мультипликативной, тогда она выражается уравнением y = x₁*x₂*. *x_k

Пример: Фонд оплаты труда = Численность работников * Среднюю зарплату.

— Аддитивной, тогда она выражается уравнением y = x₁+x₂+. +x_k

x₁ – число работников, занятых физическим трудом,

2. Индивидуальные и сводные индексы

Индивидуальные индексы получают в результате сравнения одноименных явлений, составных частей сложного явления. Например, индекс цен на подсолнечное масло определяется как отношение цены на него в отчетном периоде к цене базисного периода. Индивидуальные индексы представляют собой относительные величины динамики, выполнения плана, сравнения. Примеры:

Индивидуальный индекс физического объема продукции: , где

q₁ – количество продукции отдельного вида в отчетном периоде,

Индивидуальный индекс цены: , где

р₁ и р₀— цены на одноименный товар в отчетном и базисном периодах.

Индексы могут быть выражены в % или коэффициентах.

Если известно, что изучаемое явление неоднородно и сравнить уровни можно только после приведения их к общей мере, применяют сводные (общие) индексы, записанные в виде агрегата. «Агрегатный» (от латинского aggrego – присоединяю) – составленный из отдельных частей.

Например, сводный индекс товарооборота: .

Базисные и цепные индексы

Применяют два способа расчета индивидуальных индексов: базисный и цепной.

Базисный: (соответствует базисному темпу изменения).

Цепной: (соответствует цепному темпу изменения).

Соотношение цепных и базисных индексов:

3. Индексы количественных и качественных показателей

Количественные (объемные) показатели характеризуют общий, суммарный размер того или иного явления (количество (физический объем) продукции в натуральном измерении, численность работников предприятия, размер посевной площади).

Качественные показатели характеризуют уровень явления в расчете на единицу совокупности (цена единицы изделия, себестоимость единицы продукции, урожайность с 1 га и др.).

Объемные и качественные показатели связаны друг с другом:

Произведение качественного показателя на связанный с ним объемный показатель дает другой объемный показатель (урожайность * посевную площадь = валовой сбор). Это свойство используется при построении и исчислении индексов.

Пример индекса количественного (объемного) показателя – индекс физического объема продукции:

q – индексируемая величина, p – соизмеритель (вес).

Правило. При индексировании объемного показателя соизмеритель (вес) фиксируется на уровне базисного периода.

Данный индекс показывает, во сколько раз изменилась стоимость продукции из-за изменения физического объема продукции.

Пример индекса качественного показателя – индекс цен:

p – индексируемая величина, – q соизмеритель (вес).

Правило. При индексировании качественного показателя соизмеритель (вес) фиксируется на уровне отчетного периода.

Данный индекс показывает, во сколько раз изменилась стоимость продукции из-за изменения цены на единицу продукции.

4. Индексы переменного, фиксированного состава и структурных сдвигов

Общей характеристикой качественных показателей является средняя величина. В случае, если при изучении динамики средних показателей выявляют изменение не только усредняемого признака, но и изменение состава или структуры совокупности, необходимо применять индексы постоянного и переменного состава.

Индекс переменного состава характеризует изменение и усредняемой величины и структуры совокупности:

Индекс средней урожайности (перем. сост.) .

Если зафиксировать изменение структуры посевных площадей на уровне базисного периода, получим индекс постоянного состава:

Индекс средней урожайности (пост. сост.) .

Данный индекс характеризует изменение валового сбора под влиянием изменения средней урожайности и при неизменности структуры посевных площадей.

Индекс структурных сдвигов:

Индекс структурных сдвигов показывает, как изменилась изучаемая величина под влияние изменений в структуре совокупности.

Пример индекса переменного состава: сводный индекс товарооборота

Примеры индексов постоянного состава:

Агрегатные индексы цен:

Формула Паше (с весами отчетного периода) .

Формула Ласпейреса (с весами базисного периода) .

Рассматривая индексы, можно заметить взаимосвязь между ними:

1) взаимосвязь между цепными и базисными индексами.

2) взаимосвязь между индексами постоянного и переменного состава:

, т.е.

Данное соотношение используется при проверке результатов решения задач.

3) Если А = p*q, то I_A = Ip *Iq, ∆А = ∆Аp + ∆Aq.

Зная зависимость между величинами, можно построить систему индексов.

1. Что называется индексом?

2. Что называется индивидуальным индексом?

3. Что называется агрегатным индексом?

4. Что называется индексируемой величиной?

5. Что называется весом индекса?

6. Что показывает индекс цен?

7. Что показывает индекс физического объема продукции?

Источник

СТАТИСТИЧЕСКИЕ ИНДЕКСЫ

Поможем написать любую работу на аналогичную тему

Само слово «индекс» (index) означает показатель. Обычно этот термин используется для некоторой обобщающей характеристики изменений. Например, индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т.д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ.

В практике статистики индексы, наряду со средними величинами, являются наиболее распространенными статистическими показателями. Но индексы имеют три принципиальных отличия.

Во-первых, индексы позволяют измерить изменение сложных явлений (неоднородных статистических совокупностей). Например, нужно определить, как изменились за год расходы жителей г. Луганска на городской транспорт. Для ответа на этот вопрос необходимо знать численность пассажиров, перевезенных за год каждым видом транспорта, рассчитать среднемесячную численность пассажиров или взять точные данные из отчетов по месяцам, умножить численность на тариф перевозки (и число месяцев его действия – в случае использования среднемесячной численности) и полученные величины просуммировать. То же нужно сделать по данным за прошлый год. Затем сопоставить сумму расходов за последний год с суммой за прошлый год. То есть это не просто средние двух чисел, как при расчете, например, темпов динамики или приростов, а получение и сравнение некоторых агрегатированных величин.

Во-вторых, индексы позволяют проанализировать изменения – выявить роль отдельных факторов. Например, можно определить, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров, изменения тарифов, наконец, за счет соотношения в объеме перевозок разными видами транспорта.

В-третьих, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами. Например, интересно знать, не только как изменилось среднедушевое потребление мяса в Украине в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого потребления мяса в Украине и в развитых странах Запада, Востока. А также провести сравнение с нормативной величиной, отвечающей нормам рационального питания. Очевидно, что каждое направление сравнения вносит что-то новое.

Существует множество определений индекса.

Индекс – это показатель сравнений двух состояний одного и того же социально-экономического явления и представляет собой относительную величину, получаемую в результате сопоставления уровней сложных явлений во времени, в пространстве или с планом.

Индекс – это показатель, который сочетает в себе качества средних и относительных величин одновременно Обычно их применяют для характеристики сложных совокупностей единиц наблюдения, то есть состоящих из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости. Например, в магазине ассортимент товаров состоит из разновидностей, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, консервы – в банках, торты – в штуках, макароны – в пачках и т.д. Для определения общего объема реализации продуктов суммировать данные разнородные товары в натуральных единицах их учета, просто, нельзя, так как результат будет бессмысленным. Для получения обобщающих показателей в сложных статистических совокупностях необходимо применять индексный метод.

Индексный метод представляет собой совокупность приемов, которая исторически возникла для измерения динамики социально-экономических явлений. Это сравнительно молодой метод в статистике. В простейшей форме его стали применять более 100 лет тому назад, но по-настоящему этот метод начал развиваться значительно позднее, когда появились большие теоретические работы и практические исследования в этой области.

Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.

В зависимости от степени охвата и характера подвергнутых обобщению единиц изучаемой совокупности все индексы, употребляемые в статистике, делятся на два класса: индивидуальные (элементарные) и общие (сложные).

Индивидуальные индексы – это относительные числа, характеризующие изменения во времени показателей, относящихся к однородному объекту (к одной статистической совокупности), или изменения во времени показатели одновременно существующих однородных объектов (изменения уровней однотипных явлений). Индивидуальные индексы вычисляются просто. Если, например, требуется показать динамику цены или производительности труда, урожайности пшеницы или любой другой культуры с помощью индивидуальных индексов, то берут величину текущего периода и делят ее на величину сравниваемого периода.

Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц сложной статистической совокупности или изменение сложных общественных явлений во времени.

Рис. 13.1. Классификация статистических индексов

Общие индексы подразделяются на индексы объемных и качественных показателей.

К объемным показателям относятся:

— физический объем продукции (обозначается буквой ). Выражается в натуральных единицах объема: кг, литры, метры, мешки, банки, ящики;

— объем продукции или услуг (товарооборот), выраженный в стоимостной форме (обозначается буквами ). Выражается в денежной форме: грн., доллар.

К качественным показателям относятся:

— цена продукции или услуг (обозначается буквой ). Выражается в денежной форме: грн., доллар;

— себестоимость продукции или услуг (обозначается буквой ). Выражается в денежной форме: грн., доллар;

— затраты на производство продукции (обозначается буквами ). Выражается в денежной форме: грн., доллар.

При вычислении индексов различают сравниваемый уровень (отчетный период), и уровень, с которым производится сравнение, называемый базисным. Если показатель относится к сравниваемому (отчетному) уровню, то индексируемой величине присваивается символ «1» (например, – цена товара за отчетный период), а если показатель относится к базисному периоду, то индексируемой величине присваивается символ «0» (например, — объем продукции за базисный период).

Выбор базы сравнения определяется целью исследований. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком-либо периоде, предшествующем отношению. При этом возможны два способа расчета индексов – цепной и базисный.

Цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.

Базисные индексы получают сопоставлением текущих уровней с уровнем периода, принятого за базу сравнения, т.е. база сравнения остается неизменной.

При использовании индексов как показателей выполнения плана, за базу сравнения принимаются плановые показатели.

В статистике индивидуальные индексы принято обозначать буквой «», а общие индексы – буквой «».

Рассмотрим порядок вычисления индивидуальных индексов. Как уже отмечалось, индивидуальные индексы определяются как отношение уровня исследуемого показателя за отчетный период к уровню того же показателя за базисный период. При этом основным элементом индексного отношения является индексируемая величина, под которой понимается значение показателя за отчетный период. Ее всегда записывают в числителе индексного отношения.

Индивидуальные индексы объема реализации или производства товаров определяют по формуле:

(13.1)

где – индивидуальный индекс объема продукции;

– объем продукции в текущем (отчетном) периоде;

– объем продукции в базисном периоде.

Индивидуальные индексы цены продукции или услуг определяются по формуле:

(13.2)

где – индивидуальный индекс цены продукции;

и – цена продукции в текущем (отчетном) и базисном периодах;

Индивидуальный индекс себестоимости продукции определяется по формуле:

(13.3)

где – индивидуальный индекс себестоимости продукции;

и – себестоимость продукции в текущем (отчетном) и базисном периодах;

Пример. Пусть предприятие во II квартале 2000 года изготовило 100 утюгов, которые реализовало по цене 60 грн. за 1 шт. При этом себестоимость изготовления утюгов равнялась 40 грн. за 1 шт. Во II квартале 2001 года это предприятие изготовило только 90 утюгов и реализовало их по цене 70 грн. за 1 шт. При этом себестоимость производства утюгов достигла 45 грн. за 1 шт.

Вычислим индивидуальные индексы объема, цены и себестоимости производства утюгов.

;;

На данном предприятии во II квартале 2001 г. по сравнению с тем же периодом 2000 г:

объем производства снизился на;

но при этом возросла цена продукции на ;

а себестоимость – возросла на .

Индивидуальные индексы для статистических исследований вычисляются крайне редко, так однородных совокупностей практически не бывает.

Основной формой общих индексов являются агрегатные индексы («aggrega» (лат.) – присоединять). В числители и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых сложных статистических совокупностей.

Для достижения сопоставимости разнородных единиц в сложных статистических совокупностях в индексные соотношения вводят специальные сомножители – так называемые, соизмерители. Они необходимы для перехода от натуральных измерений разнородных единиц к однородным показателям. При этом в числителе и знаменателе общего индекса изменяются лишь значения индексируемой величины, а их соизмерители остаются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода). Это необходимо для того, чтобы на величине индекса называлось лишь влияние фактора, который определяет изменения индексируемой величины.

(13.4)

Цена является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема () и обозначение его периода берем по числителю обозначения периода вычисления цены () (отношение цены в отчетном периоде к базисному ).

Общий индекс физического объема.

(13.5)

Физический объем является количественным показателем, поэтому соизмерителем берем качественный показатель цены () и его период берем по знаменателю обозначения периода вычисления физического объема () (отношение физического объема в отчетном периоде к базисному )

Общий индекс себестоимости..

(13.6)

Себестоимость является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема () и обозначение его периода берем по числителю обозначения периода вычисления себестоимости () (отношение себестоимости в отчетном периоде к базисному )

Общий индекс товарооборота.

(13.7)

Общий индекс затрат на производство.

(13.8)

Рассмотрим индексный метод изучения динамики сложных статистических совокупностей на примерах.

Пример. Пусть имеются сведения о ценах и реализации товаров за два периода. Эти данные приведены в табл. 13.1.

Как видно из табл. 13.1, совокупность товаров разнородная (единицы измерения). Определим агрегатный индекс цен.

,

II период (отчетный)

Цена за единицу товара, грн., ()

Количество товара, ()

Цена за единицу товара, грн., ()

Количество товара, ()

Физического объема,

Источник