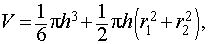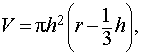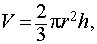Сфера что это такое в геометрии

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Круг – это часть плоскости, ограниченная окружностью.

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

– уравнение сферы радиуса R и центром С(x₀; y₀; z₀).

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

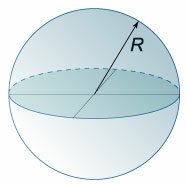
Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

.

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

Источник

Что такое шар (сфера): определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства шара и сферы, а также формулы, с помощью которых можно найти площадь поверхности и объем данных геометрических фигур.

Определение шара и сферы

Шар – это совокупность всех точек в трехмерном пространстве, которые находятся на расстоянии не больше заданного от точки, называемой центром шара (на рисунке ниже – это точка O). Другими словами, это совокупность точек, ограниченных сферой.

Шар образуется путем вращения круга вокруг своего диаметра (оси) на 180° или полукруга – на 360°.

Сфера – это поверхность шара. Образуется путем вращения окружности вокруг своего диаметра на 180° или полуокружности – на 360°.

Различают два вида шаров:

Радиус шара (сферы) – расстояние между центром и точками, лежащими на его поверхности. На рисунке выше обозначен буквой R.

Диаметр шара (сферы) – отрезок, проходящий через центр шара и соединяющие две противоположные точки на его поверхности. Совпадает с осью шара, обычно обозначается буквой d.

Полюсы шара (сферы) – точки A и B, расположенные на концах его диаметра.

Свойства шара и сферы

Свойство 1

Любое сечение шара плоскостью является кругом.

Свойство 2

Любое сечение сферы плоскостью является окружностью.

Свойство 3

Все точки сферы равноудалены от ее центра.

Свойство 4

Сфера имеет самый большой объем среди всех фигур в пространстве, имеющих одинаковую площадь поверхности.

Свойство 5

Через две любые диаметрально противоположные точки (максимально отдаленные друг от друга точки на окружности) можно провести неограниченное количество кругов для шара или окружностей для сфер радиусом, равным радиусу шара/сферы.

Примечание: если точки не диаметрально противоположны, то провести можно только один круг (окружность).

Части шара

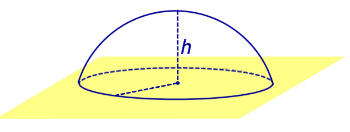
Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом. На рисунке ниже окрашен в зеленый цвет.

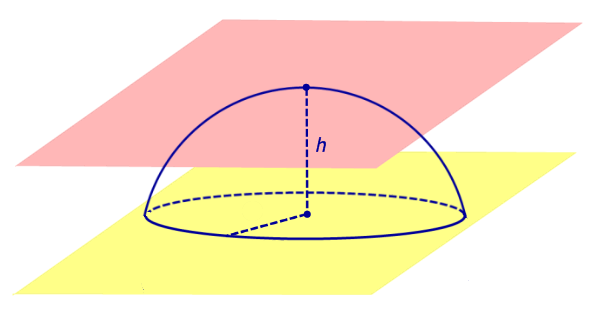
Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем. На рисунке ниже закрашен желтым.

Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента. На рисунке ниже сектор залит оранжевым.

Формулы для шара/сферы

В формулах ниже используется как радиус (R), так и диаметр фигур (d). Число π в расчетах обычно округляется до двух знаков после запятой и приблизительно равняется 3,14.

Источник

Сфера

Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252.96 кв. градусов.

Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара.

Объёмы цилиндра, вписанной в него сферы, касающейся его основания, и двух конусов, имеющих общую вершину в центре основания и основания, равные основаниям цилиндра, находятся в соотношении 1:2:3 [1]

Содержание

Основные геометрические формулы

Сфера в трёхмерном пространстве

где — координаты центра сферы, — её радиус.

Параметрическое уравнение сферы с центром в точке :

где и

Геометрия на сфере

Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие круги являются геодезическими линиями на сфере; любые два из них пересекаются в двух точках.

Расстояние между двумя точками на сфере

Если даны сферические координаты двух точек, то расстояние между ними можно найти так:

Однако, если угол задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:

В этом случае и называются широтами, а и долготами.

n-мерная сфера

В общем случае уравнение (n-1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:

где — центр сферы, а — радиус.

Пересечением двух n-мерных сфер является n-1-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.

В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.

n-мерная инверсия переводит n-1-мерную сферу в n-1-мерную сферу или гиперплоскость.

См. также

Примечания

Полезное

Смотреть что такое «Сфера» в других словарях:

СФЕРА — (греч. sphaira шар). 1) твердое тело, в котором все точки поверхности одинаково отдалены от внутренней точки, называемой центром шар; изображение земли в виде глобуса. 2) часть пространства, в котором планета совершает свой путь. 3) в фигуральном … Словарь иностранных слов русского языка

СФЕРА — жен., греч. шар, шарообразное тело или пустота, или изображенье его на бумаге; в приложении к небесным телам: шар обращаемый на оси своей, представляющий землю нашу, или небесную твердь, с означеньем всех воображаемых кругов. Армилярная сфера,… … Толковый словарь Даля

сфера — ы, ж. sphère f. <гр. sphaira. 1. геом. Замкнутая поверхность, все точки которой одинаково удалены от одной точки (центра /. БАС 1. | перен. Сфер десять пролетев воздушных, Узрел вдали питейный дом. И. Наумов Ясон. // Ирои комич. поэма 560. 2.… … Исторический словарь галлицизмов русского языка

СФЕРА — сферы, жен. [греч. sphaira шар]. 1. То же, что шар (мат.). 2. перен. Область, место, пределы, в к рых существует, действует, развивается, применяется что н. (книжн.). «Смотря по свойству поэтического таланта и по степени его выработанности, сфера … Толковый словарь Ушакова

СФЕРА — СФЕРА, ы, жен. 1. Область, пределы распространения чего н. С. деятельности. С. влияния. 2. Среда, общественное окружение. В своей сфере. Высшие сферы (о правящих, аристократических кругах). 3. Замкнутая поверхность, все точки к рой равно удалены… … Толковый словарь Ожегова

сфера — См. область … Словарь синонимов

Сфера — (Хабаровск,Россия) Категория отеля: 3 звездочный отель Адрес: Переулок Дежнева 15, Хабаровск … Каталог отелей

-сфера — сфера компонент сложных слов, означающих: 1) одну из оболочек планет и звёзд: астеносфера атмосфера барисфера биосфера геосфера гетеросфера гидросфера гомосфера ионосфера литосфера магнитосфера мезосфера стратосфера субстратосфера… … Википедия

СФЕРА — (от греческого sphaira шар), 1) область действия, пределы распространения чего либо (например, сфера влияния). 2) Общественное окружение, среда, обстановка … Современная энциклопедия

СФЕРА — (от греч. sphaira шар) 1) область действия, пределы распространения чего либо (напр., сфера влияния).2) Общественное окружение, среда, обстановка … Большой Энциклопедический словарь

СФЕРА — замкнутая поверхность, все точки которой одинаково удалены от одной точки (центра сферы). Отрезок, соединяющий центр сферы с какой либо ее точкой (а также его длина), называется радиусом сферы. Площадь поверхности сферы S=4?R2, где R радиус сферы … Большой Энциклопедический словарь

Источник

Сфера что это такое в геометрии

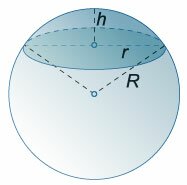
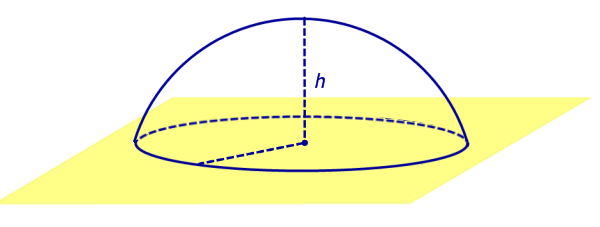
Шаровым сегментом называется часть шара, отсекаемая плоскостью.

Соотношение между высотой и радиусом основания сегмента и радиусом шара
\(R = \large\frac <<+ >><<2h>>\normalsize\),
где \(h\) − высота сегмента, \(r\) − радиус основания сегмента, \(R\) − радиус шара.

Площадь основания шарового сегмента
\(>> = \pi \)

Площадь внешней поверхности шарового сегмента
\(>> = \pi \left( <+ > \right) \)

Площадь полной поверхности шарового сегмента
\(S = >> + >> = \pi \left( <+ 2> \right) = \pi \left( <2Rh + > \right) \)

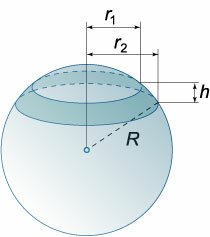
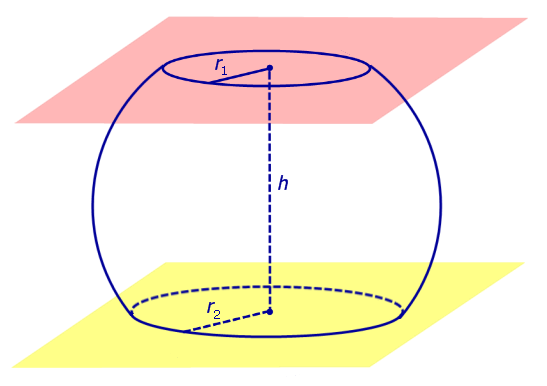
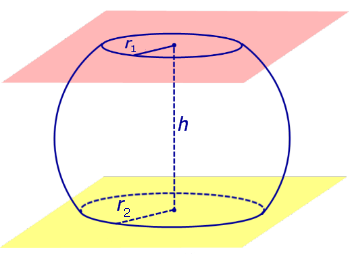
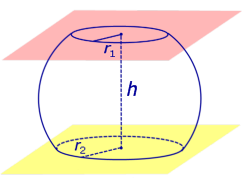
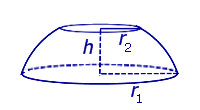
Шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями.

Площадь внешней поверхности шарового слоя
\(>> = 2\pi Rh\),
где \(h\) − высота шарового слоя, \(R\) − радиус шара.

Площадь полной поверхности шарового слоя
\(S = >> + + = \pi \left( <2Rh + r_1^2 r_2^2>\right)\),
где \(h\) − высота шарового слоя, \(R\) − радиус шара, \(\), \(\) − радиусы оснований шарового слоя, \(\), \(\) − площади этих оснований.

Объем шарового слоя
\(V = \large\frac<<\pi h\left( <3r_1^2 + 3r_2^2 + > \right)>><6>\normalsize\),
где \(\), \(\) − радиусы оснований шарового слоя, \(h\) − его высота.

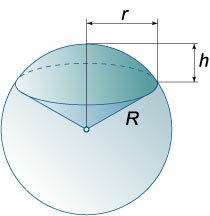
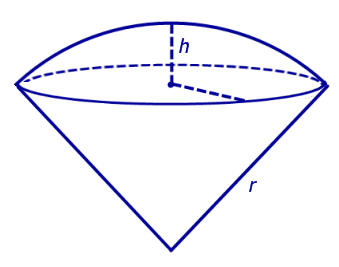
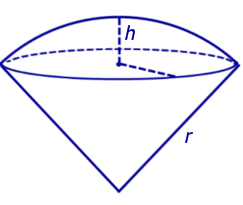
Шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше полушара.

Площадь полной поверхности шарового сектора
\(S = \pi R\left( <2h + r>\right)\),
где \(h\) − высота соответствующего шарового сегмента, \(r\) − радиус основания шарового сегмента (или конуса), \(R\) − радиус шара.

Объем шарового сектора
\(V = \large\frac<<2\pi h>><3>\normalsize\)

Источник

Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей

Шар, сфера и их части

Введем следующие определения, связанные с шаром, сферой и их частями.

Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).

Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).

Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.

Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).

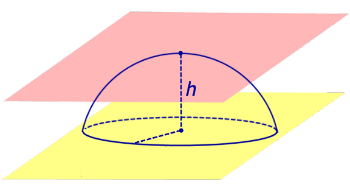
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

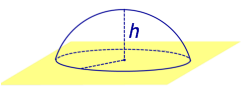
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

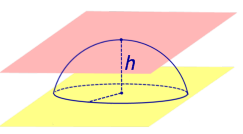
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

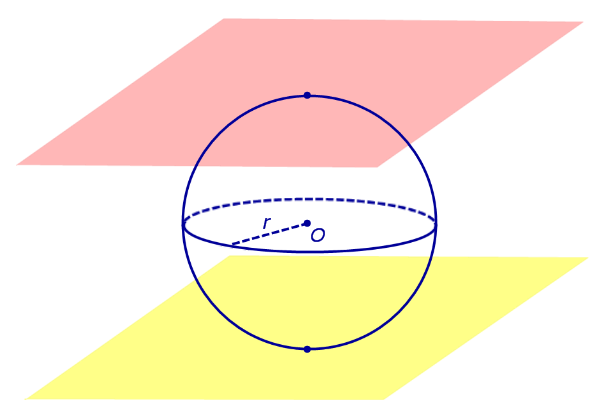
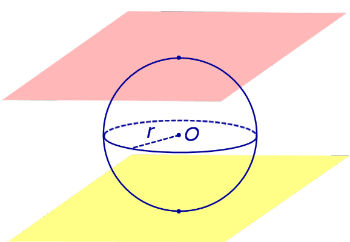
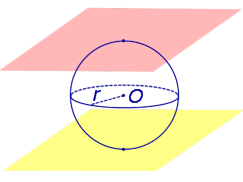
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).

Площади сферы и ее частей. Объемы шара и его частей

В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.

где
r – радиус сферы.

где
r – радиус шара.

Фигура	Рисунок	Формула	Описание
Сфера		Объем шарового сектора

где
r – радиус сферы.

Шар

где
r – радиус шара.

Сферический пояс

Площадь сферического пояса:

Источник