разделить торт на 7 частей тремя прямыми линиями
Как разрезать торт тремя прямыми так чтобы получилось 7 частей и на каждой из них была розочка?
Как разрезать торт тремя прямыми так чтобы получилось 7 частей и на каждой из них была розочка.
Если торт круглый то рисуешь линию слева вверх, от нее вправо вниз и слева направо по середине.
Край торта украшают 5 розочек из крема?
Край торта украшают 5 розочек из крема.
Торт разделили прямыми разрезами, которые прошли через каждые 2 розочки.
Сколько кусочков торта получилось.
Разрешь торт так, чтобы разрезы проходили через каждые 2 розочки, не стоящие рядом?
Разрешь торт так, чтобы разрезы проходили через каждые 2 розочки, не стоящие рядом.
Сколько кусков торта получилось?
Как разрезать торт тремя прямыми так чтобы получилось 7 частей и на каждой из них была розочка торт квадратный?
Как разрезать торт тремя прямыми так чтобы получилось 7 частей и на каждой из них была розочка торт квадратный.
Режем торт?
Круглый торт разрезали двумя прямыми разрезами.
Какое наибольшее количество частей может получиться?
Режем торт?
Круглый торт разрезали двумя прямыми разрезами.
Какое наибольшее количество частей может получиться?
Режем торт?
Круглый торт разрезали двумя прямыми разрезами.
Какое наибольшее количество частей может получиться?
Край круглого торта украшают 5 розочек из крема?
Край круглого торта украшают 5 розочек из крема.
Торт разделили прямыми разрезами, которые прошли через каждые 2 розочки.
Сколько кусочков торта получилось.
Как разделить торт тремя прямыми так, чтобы получилось семь частей и на каждой из них была розочка?
Как разделить торт тремя прямыми так, чтобы получилось семь частей и на каждой из них была розочка?
Край круглого торта украшают 5 розочек из крема?
Край круглого торта украшают 5 розочек из крема.
Торт разделили прямыми разрезами, которые прошли через каждые 2 розочки.
Сколько кусочков торта получилось?
Круглый торт разрезали с помощью трех прямолинейных разреза Так что на каждом куске оказалось ровно одна розочка могли ли на торте быть ровно 5 розочек?
Круглый торт разрезали с помощью трех прямолинейных разреза Так что на каждом куске оказалось ровно одна розочка могли ли на торте быть ровно 5 розочек.
Известно : Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
1) 6 + 0 + 0 + 1 + 3 + 4 = 14 2)5 + 0 + 5 + 0 + 5 + 1 = 16 3)1 + 1 = 2 4)6 + 0 + 0 + 3 + 0 + 4 = 13 5)1 + 3 + 1 + 9 + 0 = 14 6)1 + 4 + 4 + 3 + 0 + 0 = 12 значит 3 и 6.
Как справедливо порезать торт
Специалисты по информатике разработали алгоритм справедливого раздела пирога для любого количества людей
Двое молодых учёных, специалистов в области информатики, придумали, как честно поделить торт между любым количеством людей, решив задачу, над которой математики бились десятилетиями. Их работа удивила многих исследователей, считавших такое разделение невозможным в принципе.
Делёж пирога – это метафора для широкого круга реальных задач, включающих деление некоего непрерывного объекта, будь это торт или надел земли, между людьми, по-разному оценивающими его свойства. Одному нравится шоколадное покрытие, другой хочет получить кремовые цветочки. С библейских времён известен алгоритм деления такого объекта между двумя людьми, такой, чтобы никто не завидовал другому: один человек делит торт на две равные для него части, а другой выбирает одну из них. В Книге Бытия Авраам (тогда ещё известный, как Аврам) и Лот использовали этот метод для раздела земли, когда Авраам придумывал разделение, а Лот выбирал между Иорданом и Ханааном.
В 1960-х математики придумали алгоритм для подобного разделения пирога «без зависти» уже для трёх человек. Но до сих пор лучшим решением задачи для количества людей больше трёх была процедура, созданная в 1995 году политологом Стивеном Брамсом [Steven Brams] из Нью-Йоркского университета и математиком Аланом Тейлором [Alan Taylor] из Юнион-колледжа. Она гарантировала «справедливую» делёжку пирога, но с одним условием – процедура была «неограниченной», то есть число шагов, необходимое для делёжки, могло оказаться сколь угодно большим.
Алгоритм Брамса-Тейлора в своё время был назван прорывным, но «его неограниченность, по-моему, была большим недостатком», говорит Ариель Прокаччиа [Ariel Procaccia], специалист по информатике из Университета Карнеги-Меллон, один из создателей Spliddit, бесплатного онлайн-инструмента для справедливого раздела различных задач, от домашних обязанностей до платы за совместную аренду квартиры.
За последние 50 лет многие математики и специалисты по информатике, включая Прокаччиа, убедили себя, что ограниченного справедливого алгоритма по разделу торта на n частей не существует.
«Именно эта задача привела меня в область справедливых разделений»,- говорит Уолтер Стромквист [Walter Stromquist], профессор математики в Колледже Брина Мавра в Пенсильвании, достигший неплохих результатов в задаче делёжки торта в 1980. «Всю жизнь я думал, что я вернусь к этой задаче в свободное время и докажу, что такое расширение результата невозможно в принципе».
Но, в апреле два специалиста по информатике опровергли эти ожидания, опубликовав алгоритм справедливой делёжки торта со временем работы, зависящим от количества участников дележа, а не от их личных предпочтений. Один из учёных, 27-летний Саймон Макензи [Simon Mackenzie], доктор наук из Карнеги-Меллон, представлял свою работу 10 октября на 57-м ежегодном симпозиуме IEEE по основам информатики.
Алгоритм чрезвычайно сложный. Раздел торта между n участниками может потребовать до n n n n n n шагов, с примерно таким же количеством разрезов. Даже для небольшого количества участников это число превышает количество атомов во Вселенной. Но у исследователей уже есть идеи по упрощению и ускорению алгоритма, по словам второго участника команды, Хариса Азиза [Haris Aziz], 35-летнего специалиста по информатике из Университета Нового Южного Уэльса, работающего в австралийской группе исследования данных Data61.
Специалисты, исследующие теорию справедливого деления, по словам Прокаччиа, считают это «однозначно лучшим результатом за десятилетия».
Кусочки торта
Алгоритм Азиза и Макензи основан на элегантной процедуре, независимо придуманной математиками Джоном Селфриджем [John Selfridge] и Джоном Конвейем в 1960-х, позволяющим справедливо разделить торт на троих.
Если Алиса, Боб и Чарли (A, B, C) хотят разделить торт, алгоритм начинается с того, что Чарли делит торт на три куска, которые для него выглядят равноценными. Алиса и Боб выбирают куски, нравящиеся им. Если они выберут разные куски – вуаля, каждый получает то, что хотел.
Если Алиса и Боб выберут один кусок, тогда Боб отрезает небольшую часть от этого куска так, чтобы кусок стал равноценен, с его точки зрения, другому куску торта – тому, который бы Боб выбрал во вторую очередь. Отрезанный остаточек откладывается. Теперь Алиса должна выбрать лучший для себя кусок из оставшихся трёх, а затем выбирает Боб – с условием, что он возьмёт обрезанный им кусок, если Алиса его не выберет. Чарли получает третий кусок.
В результате никто никому не завидует. Алиса выбирала первой. Боб получил один из двух одинаково ценных для него кусков. Чарли получил один из трёх изначальных кусков, которые он резал сам.
Остаётся лишь небольшой отрезанный остаточек. Но его можно разделить, не начиная алгоритм сначала и не попадая в бесконечный цикл обрезаний и выборов, поскольку Чарли в любом случае удовлетворён своим куском – и даже если бы тот, кому достался обрезанный кусок, получил бы в довесок к нему весь остаточек целиком, для Чарли это не выглядело бы нечестным, потому что обрезанный кусок и остаточек в сумме дадут кусок торта, эквивалентный его куску – ведь он изначально сам эти куски и нарезал. Азиз и Макензи описывают такое положение Чарли, как «доминирующее».
Теперь, если, к примеру, Алисе достался обрезанный кусок, то Боб режет обрезки на три части, эквивалентные с его точки зрения, Алиса из этих кусков выбирает один себе, затем выбирает Чарли, затем Боб. Все счастливы: Алиса выбирала первой, Чарли получает кусок лучше, чем у Боба (и ему всё равно, сколько взяла Алиса), а с точки зрения Боба все три куска равноценны.
Брамс и Тейлор использовали свойство «доминирования» (но с другим именем) для разработки своего алгоритма 1995 года, но они не дожали свою идею до появления ограниченного алгоритма. В следующие 20 лет никто не добился лучших результатов. «И не из-за недостатка попыток», как говорит Прокаччиа.
Непрофессиональные делители тортов
Когда Азиз и Макензи (АиМ) решили взяться за эту задачу пару лет назад, они были новичками в задаче дележа торта. «У нас не было столько опыта, как у людей, интенсивно работавших над ней,- говорит Азиз. – Хотя обычно это недостаток, в нашем случае он был преимуществом, поскольку мы думали по-другому».
АиМ начали с изучения задачи дележа на трёх участников с нуля, и в результате анализа пришли к ограниченному справедливому алгоритму для четырёх участников, опубликованному ими в прошлом году.
Им не удалось сразу показать, как расширить свой алгоритм на число участников, большее четырёх, но они с энтузиазмом занялись этой задачей. «После отправки работы, касавшейся четырёх участников, мы очень хотели побыстрее продолжить работу, пока кто-нибудь более опытный и умный не обобщит её самостоятельно до случая с n участниками»,- говорит Азиз. И примерно через год их поиски увенчались успехом.
Как и алгоритм Селфриджа-Конвея, протокол АиМ постоянно предлагает разным участникам разрезать торт на n равных частей, а другим – делать отрезы и выбирать куски торта. Но в алгоритме есть и другие шаги, например периодический обмен кусками тортов специальным образом, с целью увеличения количества доминирующих взаимоотношений между участниками.
Эти отношения позволяют АиМ уменьшить сложность задаче. Если, допустим, три участника доминируют над остальными, их уже можно отправлять есть свои куски торта – они будут довольны вне зависимости от того, кто получит остатки. После этого остаётся меньшее число участников, и после ограниченного количества таких шагов все остаются довольными и весь торт оказывается поделён.
«Оглядываясь назад, на сложность алгоритма, становится неудивительно, что его разработка потребовала столько времени»,- говорит Прокаччиа. Но АиМ уже считают, что могут упростить алгоритм, чтобы он не требовал обмена кусками и проходил всего за n n n шагов. По словам Азиза, они уже работают над этими результатами.
Брамс предупреждает, что и у более простого алгоритма не будет практического применения – ведь куски торта, полученные участниками, будут включать множество мелких крошек с разных частей торта. Такой подход не особенно-то полезен, если вы, например, проводите раздел земли.
Но для специалистов по математике и информатике, изучающих задачу, новый результат «обнуляет всю тему», говорит Стромквист.
Азиз говорит, что исследователям теперь предстоит понять, как сократить этот разрыв. «Думаю, что в обоих направлениях может быть достигнут прогресс».
Разделить торт на 7 частей тремя прямыми линиями
РАЗРЕЗАНИЕ
Деление на неравные части (уровни 2-3).
В разделе «Разрезание многоугольников»мы делили фигуры на части одним разрезом – здесь будем делать два или три разреза. Задачи такого типа встречаются в задачниках и на олимпиадах. Форма получающихся кусков при этом обычно неважна, но важно их количество. Не стоит, пожалуй, давать эти задачи совсем маленьким – и не только потому, что нужно уверенно считать в пределах десятка. Видимо, при недостаточном жизненном опыте трудно представить себе, как будет выглядеть картинка после проведения двух прямых; поэтому попытки решения в таких случаях выглядят как хаотические, без какого-либо понимания причин неудачи.
Уровень 2.
Задача 1 Разрезать квадратный (или круглый) торт тремя прямыми линиями на 7 частей. Части не должны быть равными!
Как ни странно, эта задача может вызывать трудности. Если она, наоборот, решилась сразу – можно проверить, не случаен ли успех, попросив разделить такой же торт на 6 частей. А на 5 (это, может быть, самое трудное)? От ребят постарше можно пытаться добиться объяснений, почему круг нельзя разрезать тремя линиями больше чем на 7 частей.
Рис. 1: Разрезать торт тремя прямыми линиями на 7 кусков так, чтобы в каждом куске было по розочке.
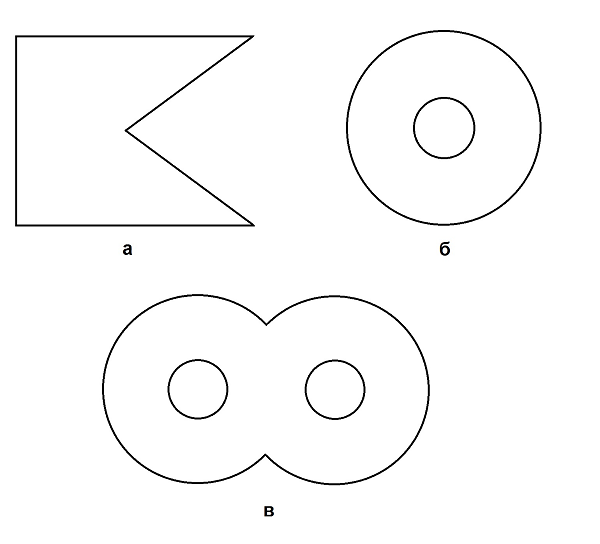
Задача 2 Разрезать флажок (рис. 2,а) двумя прямыми линиями на как можно большее число частей.
Вариации этой же задачи – разрезать толстую букву П (или Л), подкову или нарисованный валенок.
Рис. 2: Эти фигуры нужно разрезать двумя разрезами на максимальное возможное количество частей. Заметим, что ответ в задаче (в) изменится, если сделать «вырезы» более глубокими.
Задача 3 На сколько кусков возможно разделить фигуру (из рис. 2, например), сделав 2 прямых разреза?
Уровень 3.
Еще один классический вид задач на разрезание – разрезать данную фигуру на заданное число частей и собрать из них другую фигуру. Сейчас они довольно редко встречаются – возможно, из-за их сложности. Здесь мы приводим несколько задач, использующих один общий прием; это – упрощенные версии задач из книги Кордемского.
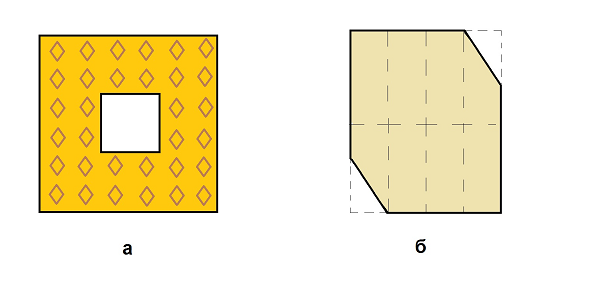
Задача 5 В квадратном коврике 3м x 3м пришлось вырезать протертую середину 1м x 1м (рис. 3,а). Как разрезать этот ковер на 2 части (не обязательно прямой линией!) и сшить из них новый прямоугольный ковер?
Рис. 3: Разрезание с последующей переклейкой: разделить на 2 части и сделать
прямоугольник.
Задача 6 Как из прямоугольной доски размером 9×4м собрать квадратную столешницу 6×6м, распилив ее всего на два куска?
Задача 7 А в этот раз нужно распилить на 2 части кусок фанеры с симметрично отрезанными углами (рис. 3,б; не обязательно пилить по прямой!) и сложить из этих частей прямоугольник.
Дополнительное упражнение – вычислить размеры полученного прямоугольника, считая размеры начального куска известными.
Как справедливо порезать торт
Специалисты по информатике разработали алгоритм справедливого раздела пирога для любого количества людей
Двое молодых учёных, специалистов в области информатики, придумали, как честно поделить торт между любым количеством людей, решив задачу, над которой математики бились десятилетиями. Их работа удивила многих исследователей, считавших такое разделение невозможным в принципе.
Делёж пирога – это метафора для широкого круга реальных задач, включающих деление некоего непрерывного объекта, будь это торт или надел земли, между людьми, по-разному оценивающими его свойства. Одному нравится шоколадное покрытие, другой хочет получить кремовые цветочки. С библейских времён известен алгоритм деления такого объекта между двумя людьми, такой, чтобы никто не завидовал другому: один человек делит торт на две равные для него части, а другой выбирает одну из них. В Книге Бытия Авраам (тогда ещё известный, как Аврам) и Лот использовали этот метод для раздела земли, когда Авраам придумывал разделение, а Лот выбирал между Иорданом и Ханааном.
В 1960-х математики придумали алгоритм для подобного разделения пирога «без зависти» уже для трёх человек. Но до сих пор лучшим решением задачи для количества людей больше трёх была процедура, созданная в 1995 году политологом Стивеном Брамсом [Steven Brams] из Нью-Йоркского университета и математиком Аланом Тейлором [Alan Taylor] из Юнион-колледжа. Она гарантировала «справедливую» делёжку пирога, но с одним условием – процедура была «неограниченной», то есть число шагов, необходимое для делёжки, могло оказаться сколь угодно большим.
Алгоритм Брамса-Тейлора в своё время был назван прорывным, но «его неограниченность, по-моему, была большим недостатком», говорит Ариель Прокаччиа [Ariel Procaccia], специалист по информатике из Университета Карнеги-Меллон, один из создателей Spliddit, бесплатного онлайн-инструмента для справедливого раздела различных задач, от домашних обязанностей до платы за совместную аренду квартиры.
За последние 50 лет многие математики и специалисты по информатике, включая Прокаччиа, убедили себя, что ограниченного справедливого алгоритма по разделу торта на n частей не существует.
«Именно эта задача привела меня в область справедливых разделений»,- говорит Уолтер Стромквист [Walter Stromquist], профессор математики в Колледже Брина Мавра в Пенсильвании, достигший неплохих результатов в задаче делёжки торта в 1980. «Всю жизнь я думал, что я вернусь к этой задаче в свободное время и докажу, что такое расширение результата невозможно в принципе».
Но, в апреле два специалиста по информатике опровергли эти ожидания, опубликовав алгоритм справедливой делёжки торта со временем работы, зависящим от количества участников дележа, а не от их личных предпочтений. Один из учёных, 27-летний Саймон Макензи [Simon Mackenzie], доктор наук из Карнеги-Меллон, представлял свою работу 10 октября на 57-м ежегодном симпозиуме IEEE по основам информатики.
Алгоритм чрезвычайно сложный. Раздел торта между n участниками может потребовать до n n n n n n шагов, с примерно таким же количеством разрезов. Даже для небольшого количества участников это число превышает количество атомов во Вселенной. Но у исследователей уже есть идеи по упрощению и ускорению алгоритма, по словам второго участника команды, Хариса Азиза [Haris Aziz], 35-летнего специалиста по информатике из Университета Нового Южного Уэльса, работающего в австралийской группе исследования данных Data61.
Специалисты, исследующие теорию справедливого деления, по словам Прокаччиа, считают это «однозначно лучшим результатом за десятилетия».
Кусочки торта
Алгоритм Азиза и Макензи основан на элегантной процедуре, независимо придуманной математиками Джоном Селфриджем [John Selfridge] и Джоном Конвейем в 1960-х, позволяющим справедливо разделить торт на троих.
Если Алиса, Боб и Чарли (A, B, C) хотят разделить торт, алгоритм начинается с того, что Чарли делит торт на три куска, которые для него выглядят равноценными. Алиса и Боб выбирают куски, нравящиеся им. Если они выберут разные куски – вуаля, каждый получает то, что хотел.
Если Алиса и Боб выберут один кусок, тогда Боб отрезает небольшую часть от этого куска так, чтобы кусок стал равноценен, с его точки зрения, другому куску торта – тому, который бы Боб выбрал во вторую очередь. Отрезанный остаточек откладывается. Теперь Алиса должна выбрать лучший для себя кусок из оставшихся трёх, а затем выбирает Боб – с условием, что он возьмёт обрезанный им кусок, если Алиса его не выберет. Чарли получает третий кусок.
В результате никто никому не завидует. Алиса выбирала первой. Боб получил один из двух одинаково ценных для него кусков. Чарли получил один из трёх изначальных кусков, которые он резал сам.
Остаётся лишь небольшой отрезанный остаточек. Но его можно разделить, не начиная алгоритм сначала и не попадая в бесконечный цикл обрезаний и выборов, поскольку Чарли в любом случае удовлетворён своим куском – и даже если бы тот, кому достался обрезанный кусок, получил бы в довесок к нему весь остаточек целиком, для Чарли это не выглядело бы нечестным, потому что обрезанный кусок и остаточек в сумме дадут кусок торта, эквивалентный его куску – ведь он изначально сам эти куски и нарезал. Азиз и Макензи описывают такое положение Чарли, как «доминирующее».
Теперь, если, к примеру, Алисе достался обрезанный кусок, то Боб режет обрезки на три части, эквивалентные с его точки зрения, Алиса из этих кусков выбирает один себе, затем выбирает Чарли, затем Боб. Все счастливы: Алиса выбирала первой, Чарли получает кусок лучше, чем у Боба (и ему всё равно, сколько взяла Алиса), а с точки зрения Боба все три куска равноценны.
Брамс и Тейлор использовали свойство «доминирования» (но с другим именем) для разработки своего алгоритма 1995 года, но они не дожали свою идею до появления ограниченного алгоритма. В следующие 20 лет никто не добился лучших результатов. «И не из-за недостатка попыток», как говорит Прокаччиа.
Непрофессиональные делители тортов
Когда Азиз и Макензи (АиМ) решили взяться за эту задачу пару лет назад, они были новичками в задаче дележа торта. «У нас не было столько опыта, как у людей, интенсивно работавших над ней,- говорит Азиз. – Хотя обычно это недостаток, в нашем случае он был преимуществом, поскольку мы думали по-другому».
АиМ начали с изучения задачи дележа на трёх участников с нуля, и в результате анализа пришли к ограниченному справедливому алгоритму для четырёх участников, опубликованному ими в прошлом году.
Им не удалось сразу показать, как расширить свой алгоритм на число участников, большее четырёх, но они с энтузиазмом занялись этой задачей. «После отправки работы, касавшейся четырёх участников, мы очень хотели побыстрее продолжить работу, пока кто-нибудь более опытный и умный не обобщит её самостоятельно до случая с n участниками»,- говорит Азиз. И примерно через год их поиски увенчались успехом.
Как и алгоритм Селфриджа-Конвея, протокол АиМ постоянно предлагает разным участникам разрезать торт на n равных частей, а другим – делать отрезы и выбирать куски торта. Но в алгоритме есть и другие шаги, например периодический обмен кусками тортов специальным образом, с целью увеличения количества доминирующих взаимоотношений между участниками.
Эти отношения позволяют АиМ уменьшить сложность задаче. Если, допустим, три участника доминируют над остальными, их уже можно отправлять есть свои куски торта – они будут довольны вне зависимости от того, кто получит остатки. После этого остаётся меньшее число участников, и после ограниченного количества таких шагов все остаются довольными и весь торт оказывается поделён.
«Оглядываясь назад, на сложность алгоритма, становится неудивительно, что его разработка потребовала столько времени»,- говорит Прокаччиа. Но АиМ уже считают, что могут упростить алгоритм, чтобы он не требовал обмена кусками и проходил всего за n n n шагов. По словам Азиза, они уже работают над этими результатами.
Брамс предупреждает, что и у более простого алгоритма не будет практического применения – ведь куски торта, полученные участниками, будут включать множество мелких крошек с разных частей торта. Такой подход не особенно-то полезен, если вы, например, проводите раздел земли.
Но для специалистов по математике и информатике, изучающих задачу, новый результат «обнуляет всю тему», говорит Стромквист.
Азиз говорит, что исследователям теперь предстоит понять, как сократить этот разрыв. «Думаю, что в обоих направлениях может быть достигнут прогресс».