как вычислить чему равен синус
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
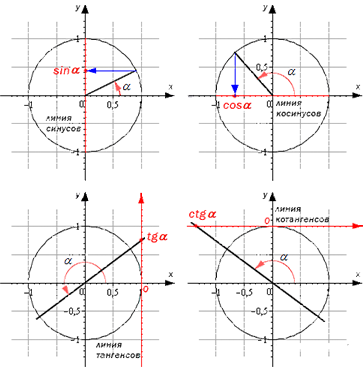
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
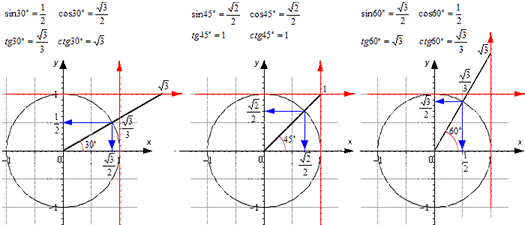
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
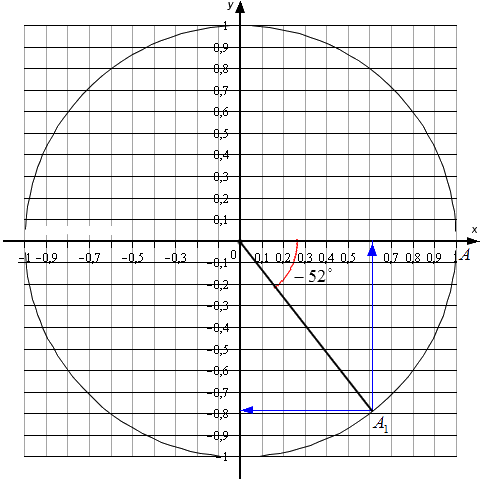
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
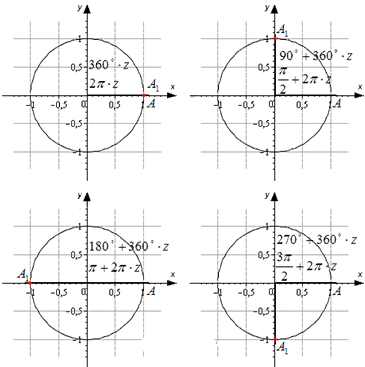
Сведение к углу
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Как посчитать синус быстро
и точно. Точнее, с заданной точностью, простите за каламбур.
Под катом я расскажу, как сделать это с использованием школьного курса алгебры и целочисленной арифметики, при чём здесь полиномы Чебышёва I-го рода, и дам ссылки на примеры реализаций для ПК и Cortex-M3.
Что же тогда делать? Увеличивать степень аппроксимации. Это позволит увеличить точность вычислений и (или) уменьшить размер таблиц. И сделать это совсем несложно.
Аппроксимация полиномами
Для примера разобьём весь период от 0 до 2π на 8 равных интервалов, и для каждого подберём такие коэффициенты A0 и A1, что бы максимум ошибки при любом аргументе был минимален (как это сделать, я расскажу ниже). Если мы построим график этого «синуса», он будет выглядеть примерно так (сплошная линия):
Штриховой линией нарисовано более точное значение синуса. А график ошибки (разницы между «настоящим» и аппроксимированным значениями будет таким:
На нём, если приглядеться, не выполняется условие «максимум ошибки при любом аргументе был минимален», но сейчас это неважно. Максимальная ошибка составляет 0.03684497.
Небольшое отступление. Числа вроде 0.03684497 или 2.448728e-09 слишком абстрактны для понимания, их трудно сравнивать. Мне, как человеку, долгое время работающему в двоичной системе, гораздо ближе биты. Поэтому к ним я и буду приводить величину ошибки, беря от неё минус логарифм по основанию 2, тогда она превращаются соответственно в 4.76 или 28.6 бит. По мне, такие логарифмические «попугаи» проще для восприятия и нагляднее. По итогам предыдущего абзаца можно сказать, что «значение синуса вычислено с точностью 4.76239 бита».
Теперь давайте разобьём один период (от 0 до 2π) не на 8, а на 64 интервала, по 16 на каждый квадрант. И рассмотрим один интервал в районе, например, 45°. График ошибки (сплошная чёрная линия) выглядит так:
Он очень похож на график параболы y = x², который нарисован там же красным штрих-пунктиром. Так же, как парабола, выглядит график полинома Чебышёва I-рода 2-й степени (более того, он ей и является). На КДПВ, он изображён голубой линией.
Красным штрих-пунктиром нарисован полином Чебышёва3-й степени, и снова оба графика очень похожи.
Здесь я открою маленький секрет. График синуса, найденный аппроксимацией функцией 2-степени по 8 интервалам, с точностью до долей пикселя совпадает с «настоящим», и, будучи нарисованными вместе, они полностью перекрывали бы друг друга. Тремя картинками выше, где нарисованы графики, сиреневым пунктиром изображён не «настоящий» синус, а полученный функцией 2-й степени.
Как сильно увеличилась точность при переходе от 1-й ко 2-й степени? Для 64 интервалов на период она возросла с 10.7 до 17.63 бит. Откуда взялись эти числа, я расскажу ниже.
Если мы дальше продолжим увеличивать степень полинома, то ошибки будут ещё меньше, и будут приобретать формы полиномов Чебышёва разных степеней:

Как считать коэффициенты
В википедии, в статье про полиномы Чебышёва есть фраза: «Многочлены Чебышёва играют важную роль в теории приближений, поскольку корни многочленов Чебышёва первого рода используются в качестве узлов в интерполяции алгебраическими многочленами«. Это как раз наш случай.
Посмотрим ещё раз на их графики:
A1·0.14645 + A0 = sin((N + 0.14645)/64 * 2π)
A1·0.85355 + A0 = sin((N + 0.85355)/64 * 2π)
Пройдясь по всем N, от 0 до 63, получим таблицу с наборами коэффициентов A1 и A0. С ней уже можно считать синус с точностью 10.7 бит. Как это делать, расскажу ниже (если кто до сих пор не понял сам).
Перейдём ко 2-й степени y = A2·x² + A1·x + A0. В качестве аргумента x подставим, соответственно, корни полинома 3-й степени 0.066987, 0.5 и 0.933013. Напишем систему из 3 уравнений с 3 неизвестными A2, A1 и A0:
A2·0.066987² + A1·0.066987 + A0 = sin((N + 0.066987)/64 * 2π)
A2·0.5² + A1·0.5 + A0 = sin((N + 0.5)/64 * 2π)
A2·0.933013² + A1·0.933013 + A0 = sin((N + 0.933013)/64 * 2π)
Решения для интервала N=15 будут следующие:
Для вычисления таблиц других размеров в предыдущую систему уравнений вместо 64 нужно подставить нужный размер. Для аппроксимации полиномом степени P нужно найти корни полинома Чебышёва степени P+1, и записать систему из P+1 уравнений с P+1 неизвестными, не забывая возводить корень многочлена в нужную степень ‘n’ при каждом An. (Если предыдущее предложение непонятно, то ничего страшного. Ближе к концу статьи будет ссылка на готовый генератор таблиц и краткая инструкция к нему.)
Точность вычислений
Разные комбинации размера таблицы и степени полинома дают разную погрешность. Не имея представления, как определить её аналитически, я решил считать «в лоб», перебирая все возможные комбинации, и прогоняя через каждую все углы от 0 до 0xffffffff. Для этого был создан проект accuracy_test. Суть в следующем:
в проект включены таблицы, степенью полинома от 1 до 6 и размером от 4 до 65536, всего 90 штук. Какие таблицы проверяем, указывается в аргументах при запуске. Можно указать набор или диапазон проверяемых таблиц;
с помощью заданной таблицы производится аппроксимация синуса по всем возможным 4294967296 аргументам. Результат аппроксимации сравнивается со значением, полученным стандартной функцией sinl(), получается разница-ошибка;
Результаты проверок всех 90 таблиц в конечном итоге сводятся в одну небольшую табличку, на основании которой строится диаграмма:
На ней видно, что с увеличением размера таблицы точность растёт, и тем быстрее, чем выше степень полинома, при этом не поднимаясь выше 54 бит. Это самая большая точность, которую мне удалось достичь, при этом вычисления производились на ПК, с помощью 80-битных чисел с плавающей точкой (long double). Почему я заострил внимание «на ПК», будет чуть дальше.
При использовании 32-битных целочисленных вычислений результаты скромнее:
Здесь точность не превышает 30.36 бит. Но с учётом того, что старший бит отведён под знак числа, ошибка получается менее самого младшего бита.
На этой диаграмме, как видно, присутствуютне все комбинации размера таблицы и степени полинома. Это связано с тем, что некоторые коэффициенты при малом количестве интервалов превышают 1, и при умножении на 0x7f000000 выходят за пределы знакового 32-битного числа. Компилятор предупреждает об этом, а попытки определить точность дают результат в районе 0 бит.
Максимальная точность на 32-битных целых числах, которую я получил, составляет 30.37 бит при множителе 0x7fffff00.
Несколько слов о вычислениях на ARM со встроенным АРМовским FPU (armhf)
Результаты неприятно удивили.
Результаты всех проверок сведены в несколько файлов, в каждом из них есть несколько листов:
О последнем надо сказать особо.
Сравним числа с плавающей точкой и какие точности на них достигнуты:
Куда делись 10 бит?
В свете этого можно рекомендовать использовать на ПК аппроксимацию вместо sinl, можно получить выигрыш во времени.
А куда же делись 10 бит, я так и не понял. Есть подозрение, что точность, равная разрядности мантиссы на 32- и 64-битных float получалась за счёт запаса 80-битных вычислений, результаты которых потом огрублялись до заданных 32 и 64, а без огрубления она как раз составляла те самые 54 бита. При вычислениях на ARMах с 64-битным FPU точность вычисления упала до 50.8 бита против 53 на x86/x64.
Таблицы с коэффициентами
В качестве аргументов программа принимает:
— размер таблицы, равный 2 n ;
— степень полинома;
— множитель для коэффициентов для приведения их к целочисленным значениям;
— параметр AC_SHIFT, показывающий, на сколько бит множитель при коэффициенте, например, 3-й степени будет «весомее» множителя предыдущей 2-й.
Результатом работы программы является исходный код на языке С. Программа выводит его непосредственно на экран, и его можно перенаправить в файл.
создаст файл sine_approx_64_3_3.c. Этот файл содержит таблицу коэффициентов для аппроксимации полиномами 3-й степени по 64 отрезкам, чего достаточно для получения 25-битной точности. Множитель при коэффициенте A0 = 0x40000000, а множители при коэффициентах более высоких степеней будут отличаться от соседних в 2³ = 8 раз.
В начале файла есть набор директив препроцессора, с помощью которых можно настраивать некоторые параметры таблицы:
Каждая строка полученной таблицы выглядит примерно так:
Как это использовать на практике
Для использования аппроксимации в своём проекте для начала нужно определиться, с какой точностью нужно вычислять синус. Потом нужно оценить ресурсы (объём памяти и быстродействие вычислителя), которые у вас есть.
К примеру, вы хотите, используя 32-битные целочисленные операции, сделать генератор с 24-битным ЦАП. Старший бит отведён на знак, поэтому точность аппроксимации должна быть не меньше 23 бит. На диаграмме видно, что заданная точность достигается при использовании:
— таблицы на 8192 строки при использовании аппроксимации 1-й степени,
— 512 строк при 2-й степени,
— 64 строки при 3-й степени,
— 32 при 4-й степени,
— 16 при 5-й степени, и
— 8 при 6-й степени.
При желании степень полинома можно увеличить ещё, длина таблицы при этом уменьшится.
Теперь следует определиться с ресурсами и приоритетами их использования. Если вы хотите получить максимальное быстродействие, нужно использовать аппроксимацию 1-й степени, при этом таблица на 8192 строки займёт 64к. Если вы используете какой-нибудь STM32 на Cortex-M3, то размещение таблицы в ОЗУ уменьшит время вычисления в отличии от размещения её в памяти программ, и у ST можно найти контроллеры с объёмом ОЗУ больше 64к.
Примеры использования
Что бы избавиться от лишних умножений для возведения в степень, формула
y = A2·x² + A1·x + A0
преобразована к виду
y = ((0 + A2)·x + A1)·x + A0
В упрощённом виде код выглядит так:
Cortex-M3
Проект на embitz для STM32F103C8.
Вычисления синуса полиномами от 1-й до 6-й степеней оформлены в виде ассемблерных вставок в код на С. Перед каждой вставкой в комментариях есть примерно измеренное кол-во тактов на 1 цикл вычислений, когда таблица находится во flash и когда в RAM, время получается разное. Размешение таблиц в оперативной памяти позволяет немного поднять быстродействие.
Я не считаю себя знатоком ARMовского ассемблера, возможно кому-то удасться вычисления ускорить.
Если второе число превысит 0x7fffffff, то оно блоком умножения будет интерпретировано как отрицательное и результат будет не тот, который мы ожидаем. Но инструкции, которая перемножала бы знаковое и беззнаковое число, в наборе команд нет. Мы будем использовать SMULL и позаботимся о том, что бы второе число не превышало 0x7fffffff, уменьшив его минимум в 2 раза. При этом надо будет после каждого умножения корректировать результат. Сделать это можно двумя способами:
— каждый раз удваивать результат, на что уйдут машинные такты;
— сделать в два раза больше то число, которое на него умножаем.
Вот и всё. Буду рад вашим замечаниям, уточнениям и предложениям.