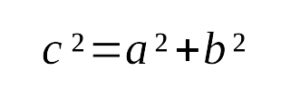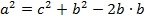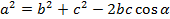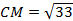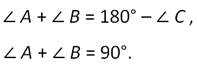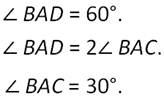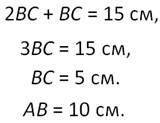как доказать что угол прямой

Прямоугольный треугольник: Признаки Равенства и Подобия

Определение

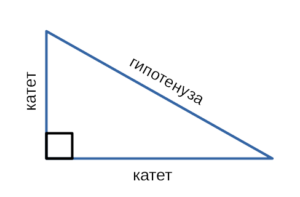
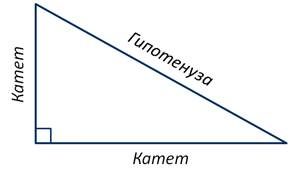
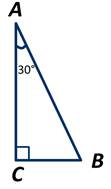
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

Формулы:

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Источник

Теорема косинусов и синусов

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

К полученному выражению прибавим и отнимем квадрат второго катета:

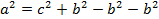
Но так как b = c * cos α, то

Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

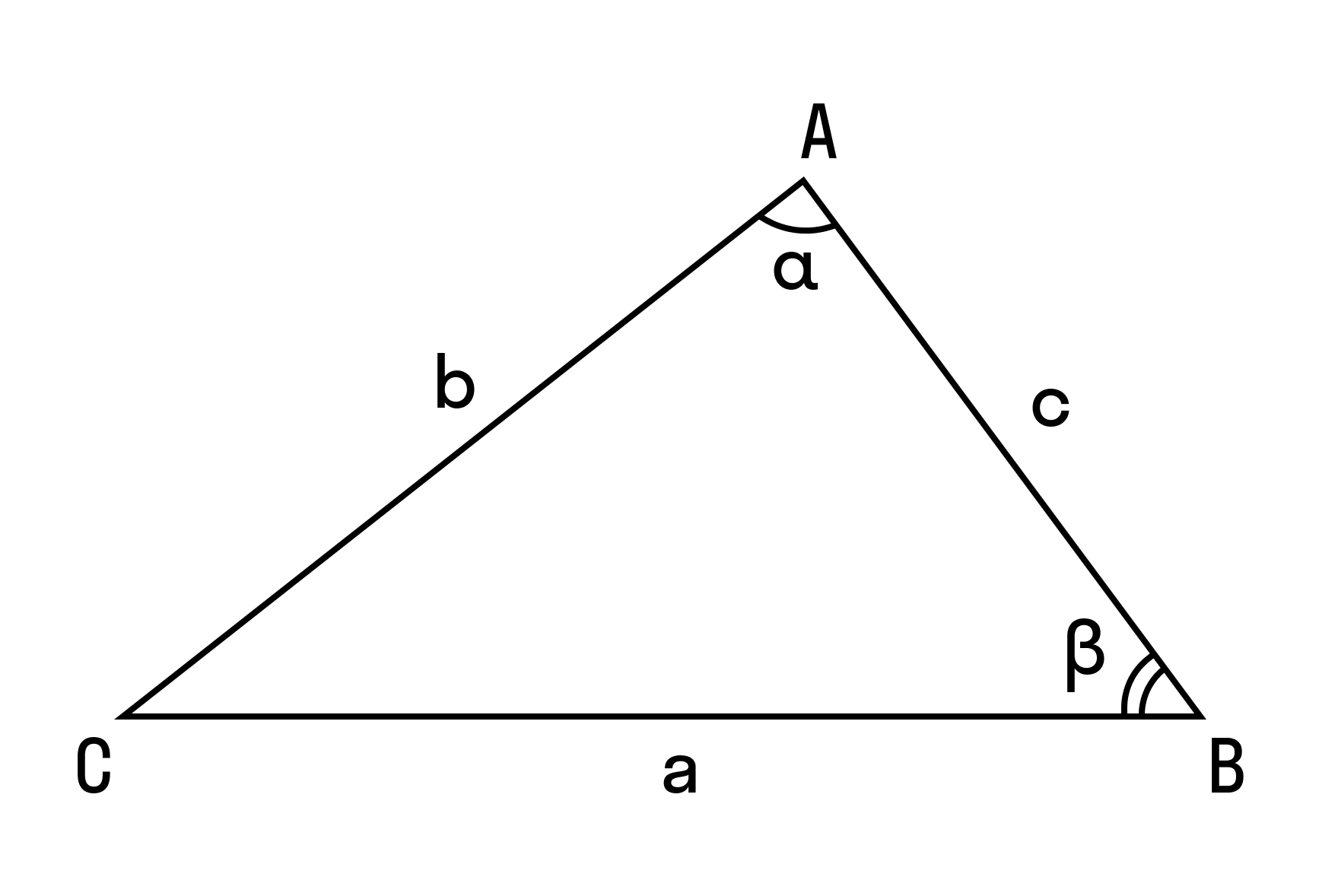
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

Приравниваем правые части уравнений:

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.

Описание формулы косинуса угла из теоремы косинусов

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Источник

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Признаки равенства прямоугольных треугольников

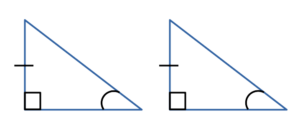
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

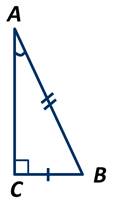
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Источник

Некоторые свойства прямоугольных треугольников

Урок 23. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Некоторые свойства прямоугольных треугольников»

Сумма углов треугольника равна 180 градусов.

Сумма двух острых углов прямоугольного треугольника равна 90 градусов.

Так как сумма углов треугольника равна 180 градусов, то:

Что и требовалось доказать.

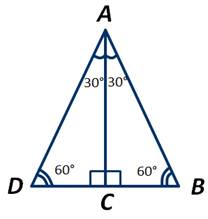
Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.

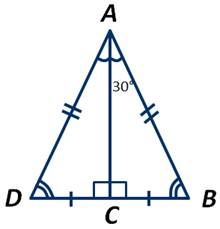
Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:

Получили, что у треугольника АВD все углы равны по 60 градусов, то есть он является равносторонним. Получаем:

Что и требовалось доказать.

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов.

Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:

Получили равносторонний треугольник АВD. Известно, что все углы равностороннего треугольника равны 60 градусам. Полуаем:

Что и требовалось доказать.

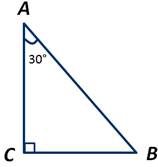
Сумма гипотенузы и катета, лежащего против угла в 30 градусов, равна 15 сантиметров. Найти длину гипотенузы.

Подставим это в предыдущее равенство и получаем:

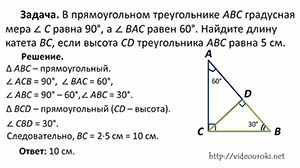
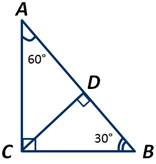
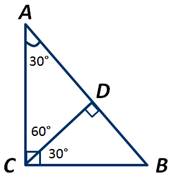
В прямоугольном треугольнике АВС, ∠С=90 градусов, а ∠ВАС=60 градусов. Найти длину катета ВС, если высота СD треугольника АСВ равна 5 сантиметров.

Рассмотрим прямоугольный треугольник АВС. ∠АСВ=90 градусов, ∠ВАС=60 градусов. А так как сумма острых углов прямоугольного треугольника равна 90 градусов, то ∠АВС=90-60=30 градусов.

Рассмотрим прямоугольный треугольник BCD:

У него ∠ВСD=30 градусов, так как по условию ВС=2*ВD.

По условию задачи ∠АСВ=90 градусов, а ∠ВСD=30 градусов, значит, ∠АСD=60 градусов.

Теперь рассмотрим треугольник АВС. У него ∠ВАС=30 градусов. Следовательно, гипотенуза АВ=2*ВС, так как катет ВС лежит против угла в 30 градусов. По условию задачи ВС=2*ВD.

Источник

Как доказать что угол прямой

Основные метрические сооьтношения в прямоугольном треугольнике

§1. Прямоугольный треугольник. Метрические соотношения.

Основные метрические сооьтношения в прямоугольном треугольнике

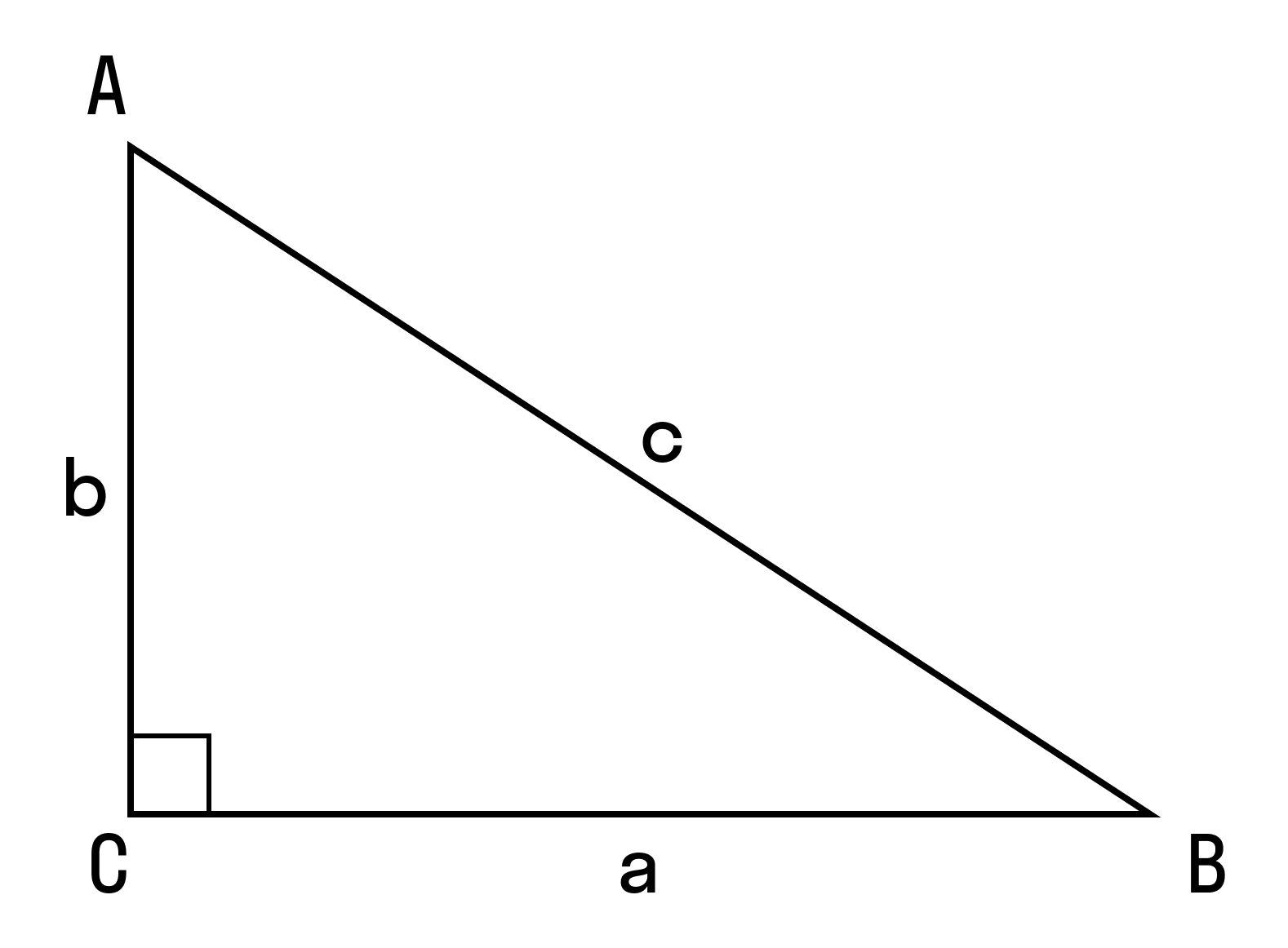
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).

Используем обычные обозначения:

`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;

`h` – высота `CD`, опущенная на гипотенузу;

`m_c` – медиана `CM`, проведённая к гипотенузе;

`R` – радиус описанной окружности;

`r` – радиус вписанной окружности.

`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.

Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

`c^2 = a^2 + b^2`

Доказательство теоремы повторите по учебнику.

Выведем ряд соотношений между элементами прямоугольного треугольника.

Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу

Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу

Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.

Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.

Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу

Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.

Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.

Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.

.

Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы

Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.

Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей

`a + b = 2(R + r)` или `a + b = c + 2r`

Равенства, доказанные в Свойствах 1 и 2, записываются также как:

Источник