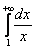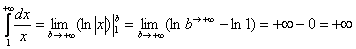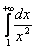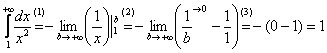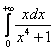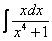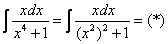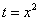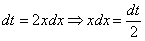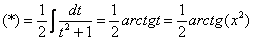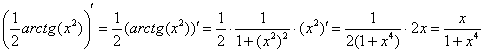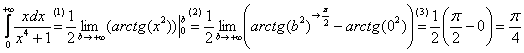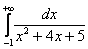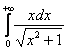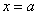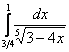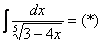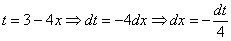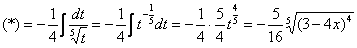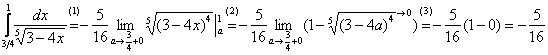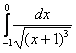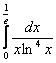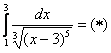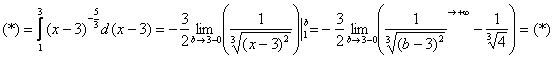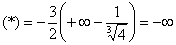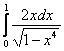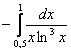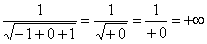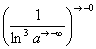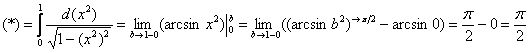как доказать что интеграл расходится
Несобственные интегралы. Примеры решений
К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 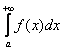
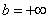
Реже встречаются интегралы с бесконечным нижним пределом 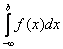
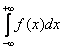
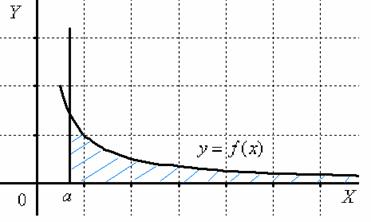
Ну а сейчас разберём самый популярный случай 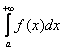
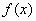
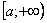
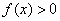
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл 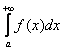
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то 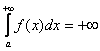
2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: 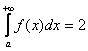
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции 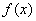
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 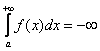
Таким образом, несобственный интеграл может быть отрицательным.
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: 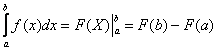
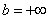
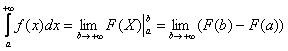
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию 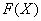
Рассмотрим два классических примера:
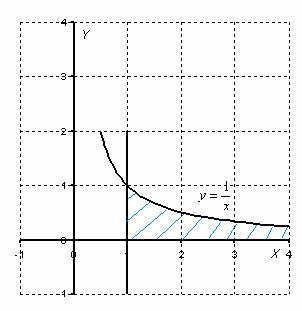
Вычислить несобственный интеграл или установить его расходимость.
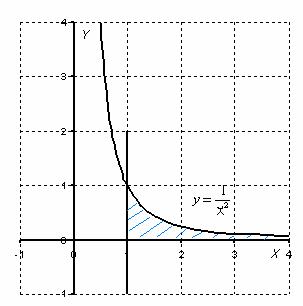
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.
Подынтегральная функция 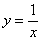
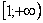
Применение нашей формулы 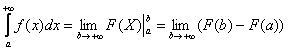
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применяется эта формула под знаком предела. Вместо привычной буквы 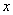
Если Вам не понятно почему 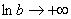
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 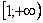
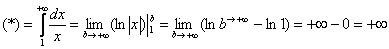
Несобственный интеграл расходится.
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция 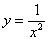
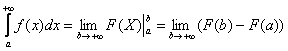
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что 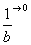
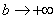
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 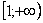
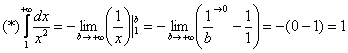
“
Что делать, если вам встретится интеграл наподобие 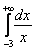
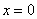
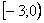
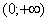
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: 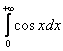
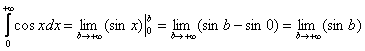
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на 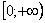
Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.
Сначала попытаемся найти первообразную функцию 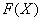
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: 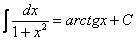
Проведем замену:
Неопределенный интеграл найден, константу 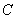
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой 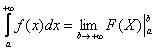
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему 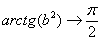
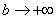
(3) Получаем окончательный ответ. Тот факт, что 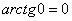
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“ 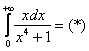
Подынтегральная функция непрерывна на 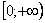
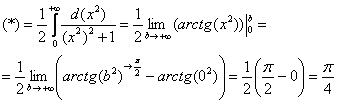
“
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 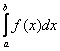
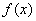
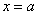
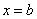
Если подынтегральной функции не существует в точке
Сразу пример, чтобы было понятно: 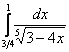
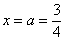
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: 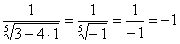
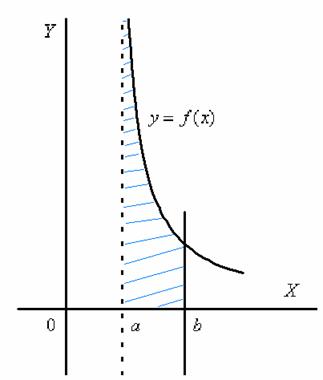
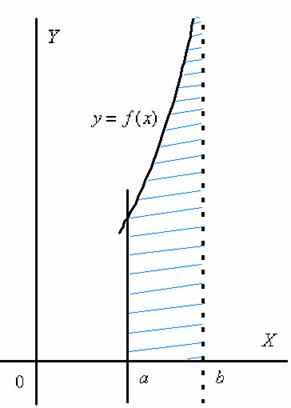
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению 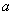
Посмотрим, как это реализуется на практике.
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 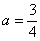
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: 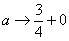
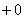
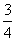
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с 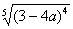
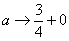
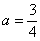
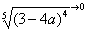
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью 
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению 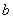
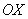
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 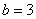
Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка 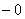
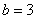
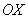
Разбираемся, почему дробь 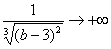
Подставляем под корень предельное значение 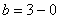
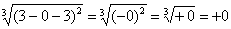
Окончательно:
Несобственный интеграл расходится.
Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но 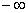
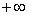
И заключительные два примера для самостоятельного рассмотрения:
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения несобственных интегралов.
Пример 4: Решение:
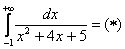
Подынтегральная функция непрерывна на 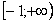

Пример 5: Решение: 
Подынтегральная функция непрерывна на 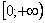
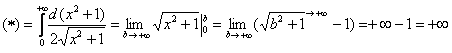
Несобственный интеграл расходится.
Пример 7: Решение: 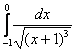
Подынтегральная функция терпит бесконечный разрыв в точке 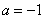
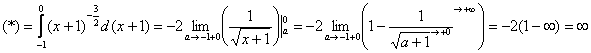
Несобственный интеграл расходится.
Примечание: с пределом выражения 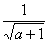
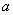
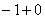
Пример 8: Решение: 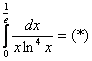
Подынтегральная функция терпит бесконечный разрыв в точке 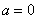
Примечание: Разбираемся в пределе выражения 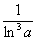
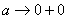
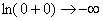
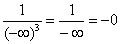
Пример 10: Решение: 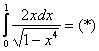
Подынтегральная функция терпит бесконечный разрыв в точке 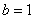
Пример 11: Решение: 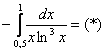
Подынтегральная функция терпит бесконечный разрыв в точке 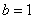
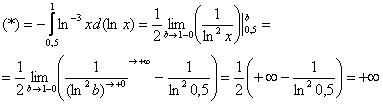
Несобственный интеграл расходится
Примечание: Разбираемся в пределе выражения 
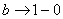
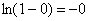
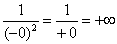
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5