как доказать что треугольники равновеликие в трапеции

Равновеликие фигуры

Презентация к уроку

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.

Решение:

5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

Решение:

III. Изучение темы «Площадь треугольника»

«Найти площадь треугольника, у которого основание a, а высота h».

Ребята, используя понятие равновеликих фигур, доказывают теорему.

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники.

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

Ответ:

3. Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S_∆ABK = 2m, ∆BCM = ∆MDK, S_ABCD = S_∆ABK = 2m.

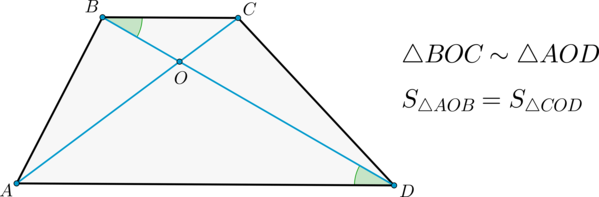
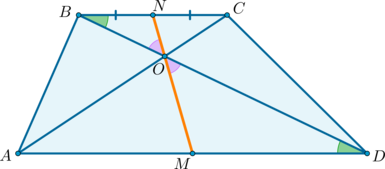
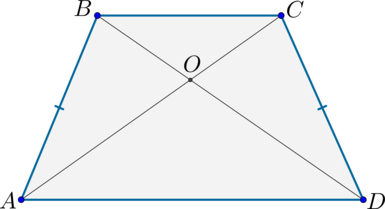
2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S_∆BCD = S_∆ABC, т.к. у них общее основание BC и одинаковая высота.

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

и , значит,

Список использованной литературы:

Источник

Трапеция

Определения

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

Теоремы: свойства трапеции

2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

Доказательство

Определение

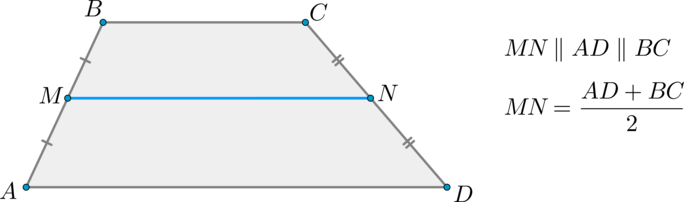
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

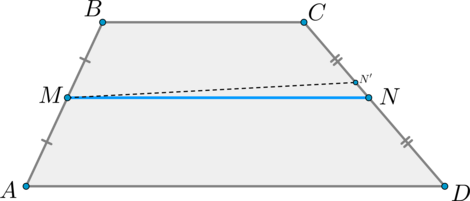
1) Докажем параллельность.

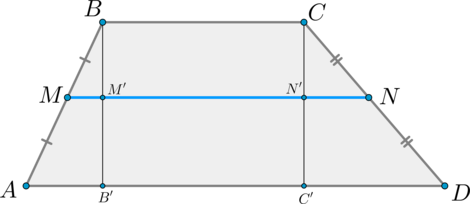
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

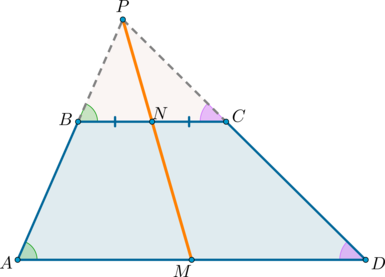
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

2) Докажем, что точки \(N, O, M\) лежат на одной прямой.

\(\triangle BNO\sim \triangle DMO\) по двум углам ( \(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac=\dfrac\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

2)

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Источник

Как доказать что треугольники равновеликие в трапеции

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

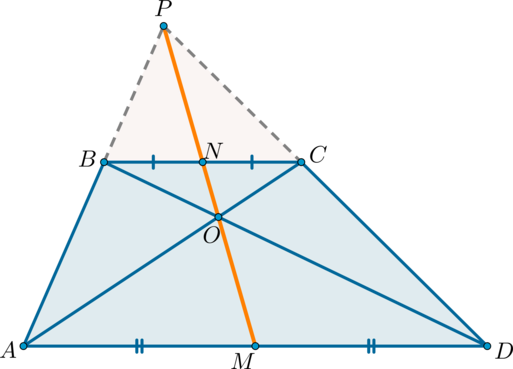
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

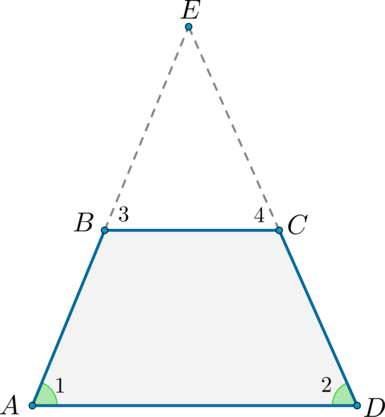
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).

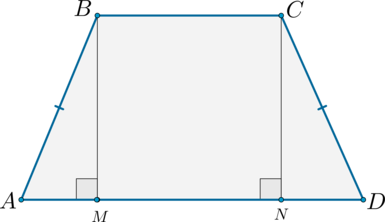
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

`d_1^2+d_2^2=c_1^2+c_2^2+2ab`.

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

Источник

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

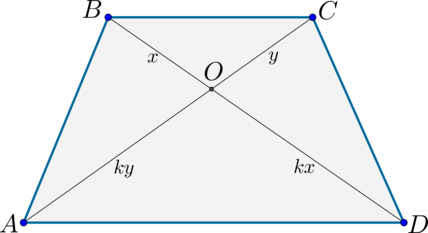
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Помогите, пожалуйста
Дана трапеция ABCD (верхнее основание BC меньше AD) с заданной S=27 и (AD/BC)=4/3. Диагонали трапеции пересекаются в точке О. Средняя линия трапеции пересекает диагонали в точке М и N.
а) Докажите, что треугольники АВО и СОD равновелики;
б) Найдите площадь треугольника MNO.

1)

При этом где – высота трапеции.
Потому и
2) Пусть
откуда
Коэффициент подобия треугольников – Тогда и высоты этих треугольников находятся в оношении То есть равны и соответственно.
Высота треугольника

Источник